Prinzip der Rekursion

Lässt sich ein Problem mit gegebenen Eingabewerten auf dasselbe Problem mit "kleineren" Eingabewerte reduzieren, kann man die Lösung des Problems rekursiv beschreiben.

Was "kleinere Eingabewerte" bedeutet, muss für das konkrete Problem definiert werden.
Wichtig ist, dass es einen kleinsten Eingabewert gibt, bei man das Problem nicht mehr weiter reduzieren muss. Denn wenn das nicht der Fall ist, kommt man in eine unendliche Rekursion und zu keiner Lösung des Problems.

Beispiel

Problem:
Wir wollen eine fix vorgegebene Basiskurve n-mal nebeneinander anordnen, wobei an einem vorgegebenen Startpunkt P mit der Zeichnung begonnen wird.

Gegeben sind daher eine natürliche Zahl n für die Anzahl der Wiederholungen und der Startpunkt P.
Gesucht ist eine Funktion f, die die fixe Basiskurve ausgehend vom Startpunkt P n-mal nebeneinander zeichnet.

Das Problem des Zeichnens der Basiskurve von einem vorgegebene Punkt aus wird dabei bereits als gelöst angesehen.
Die Basiskurve hat einen Ausgangspunkt und einen Endpunkt.

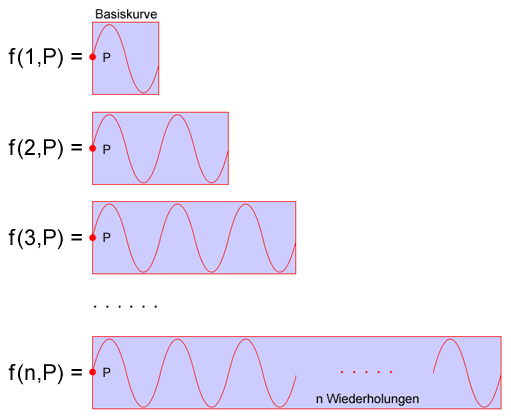
In der obigen Grafik wird schrittweise gezeigt, wie die gesuchte Funktion f für n=1, 2, 3, usw. aussieht. Diese aufzählende Beschreibung lässt sich aber auch wie folgt darstellen:

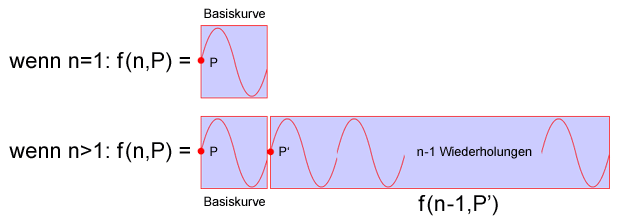
Man erkennt aus der obigen Grafik, dass sich das Problem "die Basiskurve mit n Wiederholungen von P ausgehend zu zeichnen" auf dasselbe "kleinere" Problem reduzieren lässt, bei dem nur mehr "die Basiskurve mit n-1 Wiederholungen von P' ausgehend zu zeichnen" ist. Und zwar nach folgendem Prinzip:

Um "die Basiskurve mit n Wiederholungen von P ausgehend zu zeichnen" genügt es die Basiskurve vom Punkt P ausgehend zu zeichnen und anschließend "die Basiskurve mit n-1 Wiederholungen vom Endpunkt der Basiskurve P' ausgehend zu zeichnen".

Das Problem wurde auf dasselbe kleinere Problem reduziert, von n auf n-1.
Wenn n=1 muss das Problem nicht weiter reduziert werden. In diesem Fall genügt es, die Basiskurve von P ausgehend zu zeichnen.

Diese Beschreibung ist bereits ein Algorithmus wie das Problem zu lösen ist und lässt sich unmittelbar auch in einem ActionScript-Pseudocode formulieren:

function f (n:Number, P:Point): Void {    if (n=1) {       P' = Basiskurve(P);       } else {       P' = Basiskurve(P);       f(n-1,P'); //Das ist der rekursive Aufruf der Funktion f    } } function Basiskurve(P: Point):Point {    Code für das Zeichnen der Basiskurve    return Endpunkt der Kurve;

Bemerkung

Natürlich lässt sich das obige Beispiel sehr einfach als for-Zählschleife realisieren. Aber es ging darum, an diesem einfachen Beispiel das Prinzip der Rekusion zu verdeutlichen.

Grundsätzlich gilt, dass sich jede Schleife als Rekursion darstellen lässt und umgekehrt.

Die Umwandlung einer Schleife in eine Rekusion ist ein triviales Problem. Der umgekehrte Weg, eine Rekursion in Schleifen aufzulösen, ist in der Regel ein nichttriviales Problem, denn Rekursionen können sehr komplex sein.

Viele Probleme lassen sich durch Rekursionen sehr elegant beschreiben und lösen. Bei der Abarbeitung im Computer sind Rekursion jedoch in der Regel langsamer als Schleifen, da der interne Aufwand für Zwischenspeicherungen höher ist.

Ein weiteres, etwas komplexeres Beispiel: Binärer Baum

Problem:
Es soll folgende Grafik (ein binärer Baum) gezeichnet werden:

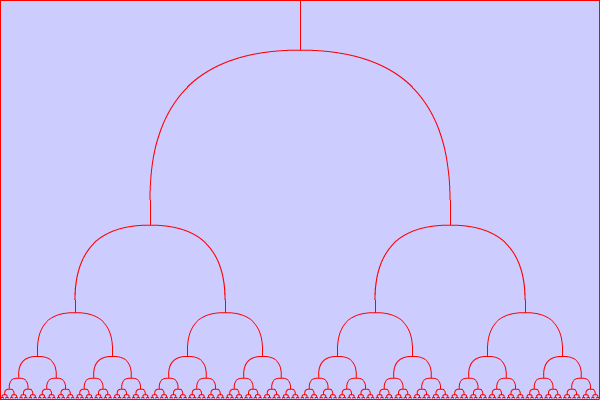
Gegeben sind dabei die Höhe a und Breite b der Basiskurve und ein Startpunkt P von dem ausgehend der binäre Baum gezeichnet wird.
Gesucht ist eine Funktion baum, die die Basiskurve mit Höhe a und Breite b ausgehend vom Startpunkt P zeichnet und an den zwei Endpunkten wieder Basiskurven mit halber Höhe und Breite zeichnet. Das soll solange fortgesetzt werden, bis eine minimale Breite der Basiskurve erreicht ist

Das Problem des Zeichnens der Basiskurve von einem vorgegebene Punkt aus wird dabei bereits als gelöst angesehen.
Die Basiskurve hat einen Ausgangspunkt und zwei Endpunkte.

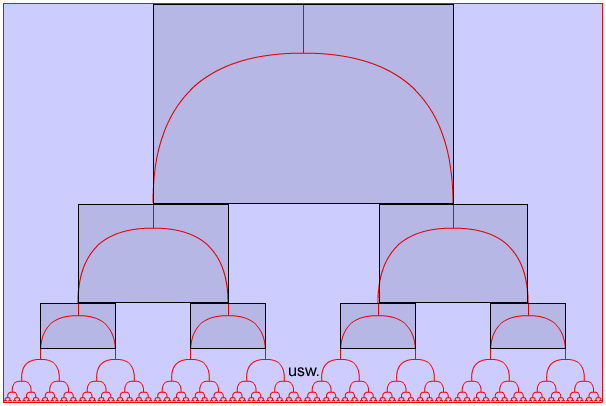
Abb.: Der binäre Baum mit den eingezeichneten, kleiner werdenden Basiskurven.

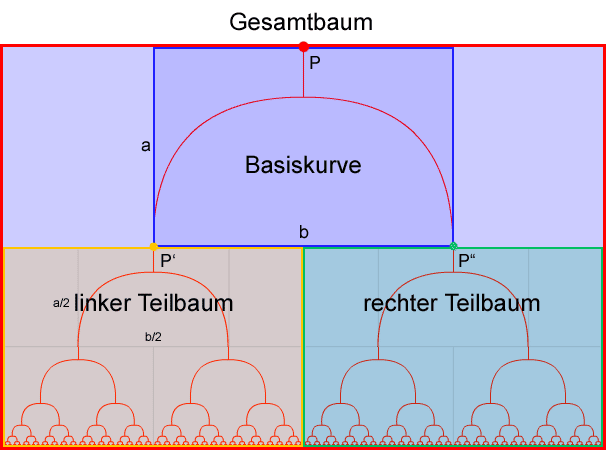
Man erkennt aus der obigen Grafik, dass sich das Problem "ausgehend vom Punkt P einen binären Baum mit einer Startbasiskurve der Höhe a und Breite b zu zeichnen" auf dasselbe "kleinere" Problem reduzieren lässt, bei dem "ausgehend von den Punkten P' und P" zwei binäre Bäume mit Startbasiskurven der Höhe a/2 und Breite b/2 zu zeichnen" sind. Und zwar nach folgendem Prinzip:

Um "ausgehend vom Punkt P einen binären Baum mit einer Startbasiskurve der Höhe a und Breite b zu zeichnen" genügt es die Basiskurve vom Punkt P ausgehend zu zeichnen und anschließend "ausgehend von den Endpunkten der Basiskurve P' und P" zwei binäre Bäume mit Startbasiskurven der Höhe a/2 und Breite b/2 zu zeichnen".

Das Problem wurde auf dasselbe kleinere Problem reduziert, von a auf a/2 (bzw. von b auf b/2).
Wenn a (bzw. b) unter einem fixen Grenzwert liegt, muss das Problem nicht weiter reduziert werden. In diesem Fall wird nichts mehr gezeichnet.

Diese Beschreibung ist wieder ein Algorithmus wie das Problem zu lösen ist und lässt sich unmittelbar auch in einem ActionScript-Pseudocode formulieren:

function baum (P:Point, a:Number, b:Number): Void {    if (a >= Grenzwert) {       var endPunkte:Array = Basiskurve(P, a, b);       var P':Point = endPunkte[0];       var P":Point = endPunkte[1];       baum (P', a/2, b/2); //Das ist der erste rekursive Aufruf der Funktion baum       baum (P", a/2, b/2); //Das ist der zweite rekursive Aufruf der Funktion baum    } } function Basiskurve(P:Point, a:Number, b:Number):Array {    Code für das Zeichnen der Basiskurve    return Array der Endpunkte der Kurve;