Wiederholtes Zeichnen eines Kurvensegments mit einer for-Schleife (Wiederholung)
Schleifen, Wiederholungen
Im vorigen Arbeitsschritt wurde für jedes Kurvensegment eine eigene Programmzeile mit speziellen x-Koordinatenwerten geschrieben.
Die y-Koordinatenwerte wurden immer in Abhängigkeit vom Wert der Variablen m definiert.
| this.curveTo(50, m-70, 100, m); |
Für 6 Kurvensegmenten ist diese Methode noch praktikabel. Aber wenn man viele Kurvensegmente nebeneinandersetzen möchte, wird es sehr mühsam.
Bei etwas genaueren Betrachtung des Codeabschnittes, erkennt man ein Muster, das sich in leichten Variationen wiederholt.
Der Grundbaustein, der in diesem Muster sechsmal wiederholt wird, ist der Code this.curveTo( ? , m ? 70, ?, m) in dem sich die x-Koordinaten und die Vorzeichen nach einer bestimmten Regel entwickeln.
Ziel ist es, diese Regel zu entdecken und zu formalisieren.
Wenn derselbe Codeabschnitt mehrmals hintereinander wiederholt werden soll, spricht man von einer Schleife.
Ganz allgemein lassen sich Schleife durch nachfolgende Ablaufdiagramme beschreiben:
while-Schleife
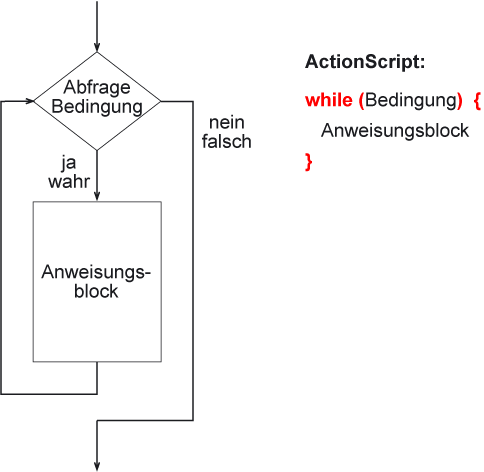
An Beginn einer while-Schleife steht immer eine Frage, die mit ja oder nein beantwortet werden kann, oder eine Bedingung, die wahr oder falsch ist.
Wenn die Frage mit Ja beantwortet wird bzw. die Bedingung wahr ist, wird der nachfolgende Anweisungsblock ausgeführt.
Anschließend wird wieder dieselbe Frage gestellt bzw. der Wahrheitswert der Bedingung abgefragt.
Dieser Vorgang wiederholt sich solange bis die Frage mit Nein beantwortet wird bzw. die Bedingung falsch ist. Man sagt, die Schleife terminiert.
Es ist daher klar, dass sich bei der Abarbeitung des Anweisungsblocks in der Schleife der (Speicher-)Zustand des Programms verändern muss, damit die Bedingung falsch werden kann.
Wenn eine Bedingung nie falsch wird, kommt es zu einer Endlosschleife, in der der Programmablauf hängen bleibt. In der Regel ist das eine unerwünschte Situtation.
Wenn bei einer while-Schleife die Bedingung gleich beim ersten Mal falsch ist, wird der Anweisungblock nie abgearbeitet. Die Anzahl der Wiederholungen sind nicht von Anfang an vorgegeben.
do-while-Schleife (repeat-Schleife)
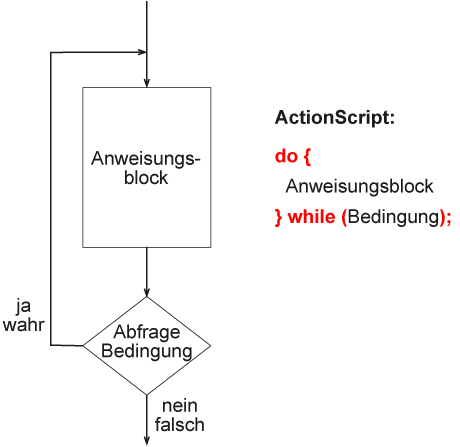
An Beginn einer do-while-Schleife (in anderen Programmiersprachen repeat-Schleife genannt) steht immer ein Anweisungsblock. Nachdem dieser mindestens einmal abgearbeitet wurde folgt eine Frage, die mit ja oder nein beantwortet werden kann, oder eine Bedingung, die wahr oder falsch ist. Wenn die Frage mit Ja beantwortet wird bzw. die Bedingung wahr ist, wird der Anweisungsblock erneut ausgeführt.
Dieser Vorgang wiederholt sich solange bis die Frage mit Nein beantwortet wird bzw. die Bedingung falsch ist. Man sagt, die Schleife terminiert.
Es ist daher klar, dass sich auch bei der Abarbeitung des Anweisungsblocks in der do-while-Schleife der (Speicher-)Zustand des Programms verändern muss, damit die Bedingung falsch werden kann.
Wenn eine Bedingung nie falsch wird, kommt es zu einer Endlosschleife, in der der Programmablauf hängen bleibt. In der Regel ist das eine unerwünschte Situtation.
Bei einer do-while-Schleife wird der Anweisungblock mindestens einmal abgearbeitet. Die Anzahl der Wiederholungen sind nicht von Anfang an vorgegeben.
Jede do-while-Schleife lässt sich auch als while-Schleife formulieren:
| do { entspricht Anweisungsblock; |
for-Schleife (als Spezialfall Zählschleife)
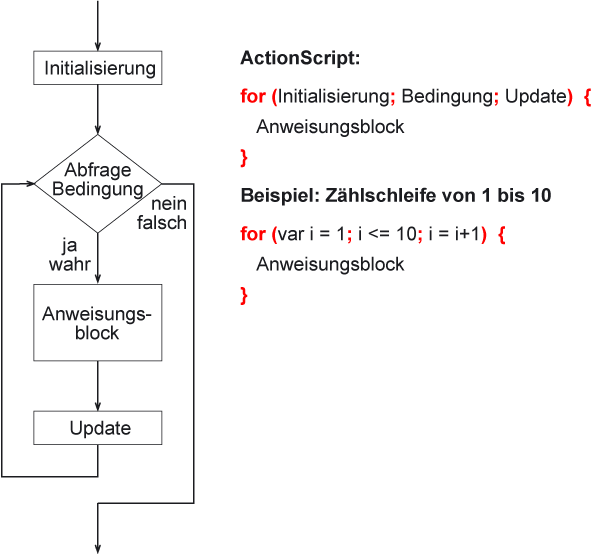
Eine spezielle Schleifenform ist die for-Schleife bei der in der Regel die Anzahl der Wiederholungen von Anfang an feststeht.
Es wird eine (Zähl-)Variable definiert, mit einem Startwert initialisiert. Anschließend definiert man, wie der Inhalt der Variablen in jedem Schleifendurchlauf verändert wird (sehr oft erfolgt ein Zählvorgang nach oben oder unten) und wann dieser (Zähl-)Vorgang beendet wird. In jedem Schleifendurchlauf wird wieder ein Anweisungblock abgearbeitet.
Jede for-Schleife lässt sich auch als while-Schleife formulieren:
| for (var i= ...; Bedingung mit i; Update von i) { entspricht var i= ...; |
Ergebnis der swf-Datei
Die Kurvenlinie wird mit Hilfe einer for-Schleife gezeichnet.
Der Programmcode ohne Erklärungen
Codeabschnitte, die sich nicht vom vorigen Arbeitsschritt unterscheiden, werden grau geschrieben.
| // BÜHNENRECHTECK MIT FARBE FÜLLEN UND KONTURIEREN |
Der Programmcode mit Erklärungen
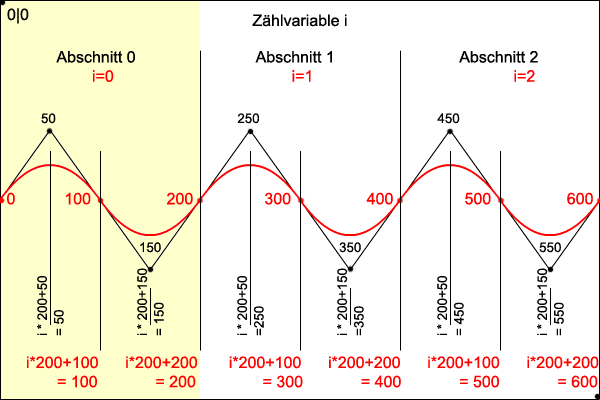
Man erkennt aus der obigen Grafik, dass die Grundkurve (gelber Abschnitt) zweimal wiederholt wird. Bei jeder Wiederholung wird die Kurve um 200 Pixel nach rechts verschoben.
Es gibt daher drei Abschnitte, die sich nur durch die schrittweise Linksverschiebung um 200 Pixel unterscheiden.
Wir führen nun eine Zähvariable i für die Abschnitte ein, die nacheinander die Werte 0, 1 und 2 annimmt. i=0 entspricht dem ersten Abschnitt ("nullte" Wiederholung, Abschnitt 0), i=1 entspricht dem zweiten Abschnitt (erste Wiederholung, Abschnitt 1) und i=2 entspricht dem dritten Abschnitt (zweite Wiederholung, Abschnitt 2).
In der Informatik beginnt der Zählvorgang sehr oft bei null und nicht wie sonst üblich bei eins.
In Abhängigkeit von der Zählvariablen kann man nun die x-Koordinaten der Anker- und Steuerpunkte ausgehend vom Startpunkt des jeweilgen Kurvenabschnitts beschreiben:
Die x-Koordinaten der Startpunkte liegen bei 0, 200 und 400, d.h. bei i * (Grundkurvenbreite) für i=0, 1 und 2.
Die jeweiligen x-Koordinaten der Steuer- und Ankerpunkte werden um 50 nach links verschoben und
liegen bei 50, 100, 150, 200 für i=0, 250, 300, 350, 400 für i=1 und 450, 500, 550, 600 für i=2, d.h. bei
i * (Grundkurvenbreite) +50, i * (Grundkurvenbreite) +100, i * (Grundkurvenbreite) +150 und i * (Grundkurvenbreite) +200 für i=0, 1 und 2.
Daraus ergibt sich folgende for-Schleife mit der Zählvariablen i vom Typ Number:
Initialisierung von i : i = 0 , wir beginnen bei null zu zählen.
Bedingung von i : Wir zählen bis 2, d.h. i muss kleiner als 3 oder kleiner-oder-gleich 2 sein, i < 3 oder i <= 2 , beide Schreibweisen sind m�glich.
Update von i : Um eins nach oben zählen, d.h. i wird um eins erhöht i = i + 1
Die h�ufig verwendete Wertzuweisung i = i + 1 wird mit i++ abgek�rzt.
Die x-Koordinaten in den curveTo-Methodenaufrufen ergeben sich aus obiger Überlegung und die y-Werte pendeln mit einer fixen Amplitude von 70 um den Wert der Variablen m.
| for (var i:Number = 0; i<3; i++) { |
 Verlauf
Verlauf
