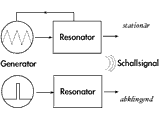
Gekoppelte Schwingungen spielen eine wesentliche Rolle in der Elektronik und Physik. Eine gekoppelte (einfache) Schwingung erhält man beispielsweise, wenn zwei Pendel elastisch so miteinander verbunden sind, dass die Auslenkung eines Pendels auch Kräfte auf das andere bewirkt, also beide nicht mehr unabhängig voneinander schwingen.
Eigenfrequenz und Schwingungsmodus
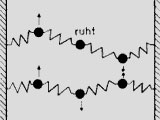
Wenn man beide Massen (P1 und P2) gleich weit und in eine Richtung aus der ihrer anfänglichen Ruhelage auslenkt, so beeinflusst die mittlere Feder die resultierenden Schwingungen nicht. Das Ergebnis kann als einfache, harmonische Schwingung mit niedriger Eigenfrequenz beschrieben werden.
Werden beide Massen wiederum gleich weit, aber in entgegengesetzte Richtung aus ihrer Ruhelage ausgelenkt, so wirkt sich nun auch die mittlere Feder auf das Schwingungsergebnis aus. Die Schwingung besitzt eine höhere Eigenfrequenz.
Auch jede andere Auslenkung der Pendel aus der Ausgangslage kann als additiv überlagerte harmonische Schwingung beschrieben werden.
Wird das System um zusätzliche Federn und Massen (Pendel) ergänzt, so erhält man für jede weitere Masse einen zusätzlichen Schwingungsmodus mit der zugehörigen Eigenfrequenz. Wie stark die Schwingungsmodi zur resultierenden Schwingung einer Masse beitragen, hängt davon ab, wie die Massen anfänglich ausgelenkt werden.
Lässt man die Anzahl der Massen gegen unendlich anwachsen, so erhält man schließlich ein Modell für eine schwingende Saite.
 Abb.: Gekoppeltes Schwingungssystem | Wenn die beiden Systeme (P1 und P2) starr aneinander gekoppelt werden, so verhält sich das System wie ein einfaches Schwingungssystem, dessen Masse sich aus der Addition der beiden Einzelmassen ergibt. Zwischen diesen beiden Fällen – elastische und starre Kopplung – wird das gekoppelte Schwingungssystem immer zwei Eigenfrequenzen aufweisen, die sich gegenseitig umso stärker beeinflussen, je stärker die Kopplung ist. Wenn durch Krafteinwirkung die beiden Pendel ins Schwingen gebracht, so setzt sich diese immer additiv aus den beiden Eigenschwingungen zusammen. |
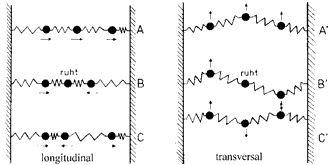 | Die Erweiterung auf eine Pendelkette ergibt longitudinale und transversale Schwingungsmodis nach den Typen A, B und C. |
Eigenfrequenz und Schwingungsmodus
Wenn man beide Massen (P1 und P2) gleich weit und in eine Richtung aus der ihrer anfänglichen Ruhelage auslenkt, so beeinflusst die mittlere Feder die resultierenden Schwingungen nicht. Das Ergebnis kann als einfache, harmonische Schwingung mit niedriger Eigenfrequenz beschrieben werden.
Werden beide Massen wiederum gleich weit, aber in entgegengesetzte Richtung aus ihrer Ruhelage ausgelenkt, so wirkt sich nun auch die mittlere Feder auf das Schwingungsergebnis aus. Die Schwingung besitzt eine höhere Eigenfrequenz.
Auch jede andere Auslenkung der Pendel aus der Ausgangslage kann als additiv überlagerte harmonische Schwingung beschrieben werden.
Wird das System um zusätzliche Federn und Massen (Pendel) ergänzt, so erhält man für jede weitere Masse einen zusätzlichen Schwingungsmodus mit der zugehörigen Eigenfrequenz. Wie stark die Schwingungsmodi zur resultierenden Schwingung einer Masse beitragen, hängt davon ab, wie die Massen anfänglich ausgelenkt werden.
Lässt man die Anzahl der Massen gegen unendlich anwachsen, so erhält man schließlich ein Modell für eine schwingende Saite.
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel