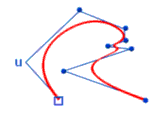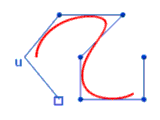
Geschichtliches
Spline: (engl.) übersetzt: das Kurvenlineal, ein längliches, dünnes Stück Holz oder Metall;
Geschichtlich gesehen gingen die B-Splines (Basis-Splines) den Bézier-Kurven voraus. Entwickelt wurden die B-Splines noch vor der Computermodellierung im Schiffsbau, wo die Designer lebensgroße Kurven zeichnen mussten. Für Zeichnungen im kleineren Maßstab verwendeten die Konstrukteure vorgefertigte Kurvenlineale. Für maßstäbliche Pläne war diese Methode jedoch ungeeignet. Die Zeichner verwendeten dafür lange, dünne Metallstreifen. Diese Streifen, auch Splines genannt, wurden in die gewünschte Form geschoben. Mit Bleigewichten, so genannte Knots, wurde die Form der Streifen fixiert. Die Fixierung bzw. Formgebung erfolgt durch "Gewichte", daher auch der Name "Gewichtsfunktionen".
Vergleich B-Splines / Bézier-Kurven
Die entscheidenden Vor- bzw. Nachteile von B-Splines gegenüber Bézier-Splines:
| B-Splines | Bézier-Kurven |
| Der Grad der Polynome ist unabhängig von der Anzahl der Kontrollpunkte. | Bei Bézier-Kurvensegmenten ist der Grad des Polynoms immer um eins niedriger als die Anzahl der Kontrollpunkte. Bei kubischen Bézier-Kurvensegmenten handelt es sich um Polynome dritten Grades mit vier Kontrollpunkten. |
| Bei B-Splines ist eine lokale Kontrolle der Kurve möglich. | Die Kontrollpunkte üben einen "globalen" Einfluss auf das Kurvensegment aus. Das Bewegen eines jeden Kontrollpunktes betrifft das ganze Kurvensegment. |
| Kontrollpunkte können beliebig verschoben werden. | Zur Bewahrung der Stetigkeit von Bézier-Kurvensegmenten ist das Bewegen von Kontrollpunkten gewissen Bedingungen unterworfen (siehe Bézier-Kurvensegmente verbinden). |
| Der de Boor-Algorithmus liefert die Auswertung der Kurve | Der Casteljau-Algorithmus liefert die Auswertung der Kurve. |
Die Art von B-Splines hängt von dem verwendeten Knotenvektor ab. Der Knotenvektor ergibt sich aus den Knotenintervallen bzw. Knotenwerten. B-Splines unterscheiden sich dadurch, dass die Knotenintervalle der einzelnen Knotenwerte entweder gleich groß sind oder variieren:
- uniforme (periodische) B-Splines
- offene uniforme B-Splines
- nicht-uniforme B-Splines
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel