Da in der Computergrafik in der Regel kubische Nurbs-Kurven eingsetzt werden, beschränken sich die weiteren Erklärungen auf kubische B-Splines.
Ein B-Spline besteht generell aus Teilen von Polynomen, die zu einer gesamten Kurve zusammengestellt werden. Die Anzahl von Kurvenabschnitten (Spans) ist beliebig. Folglich können auch beliebig viele Kurvenpunkte eingefügt werden. Bei einer kubischen B-Spline ist jeder Kurvenabschnitt durch vier Basisfunktionen und vier Kontrollpunkte definiert. die Kontrollpunkte der B-Splines haben einen sogenannten Knotenwert (u-Parameter). Diese u-Parametrisierung erstreckt sich vom Anfangspunkt bis zum Endpunkt der Kurve. Jeder Kurvenabschnitt besitzt am Anfang und am Ende einen Knotenwert. Der Verbindungspunkt beim Wert von u zwischen den Segmenten wird als Knotenwert bezeichnet.
Bei uniformen B-Splines ist der Abstand zwischen zwei Knotenwerten immer konstant. Die Gewichtsfunktionen einer uniformen B-Spline sind periodisch und folglich einfacher zu berechnen. Solche B-Splines werden als uniforme bzw. periodische B-Splines bezeichnet.
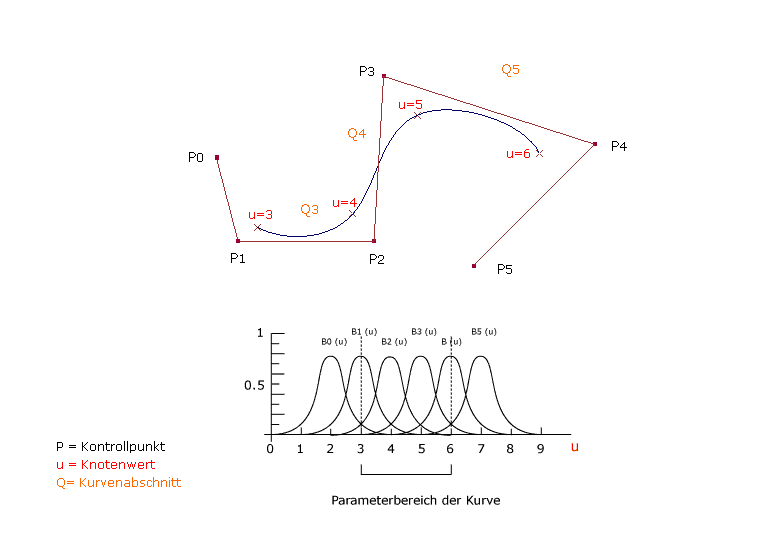 |
| Die Abbildung zeigt eine uniforme B-Spline-Kurve dritten Grades, die durch die Position von sechs Kontrollpunkten definiert ist. Jeder Kurvenabschnitt (Q) ist durch vier Kontrollpunkte beeinflusst. Da jeder Kurvenabschnitt durch vier Kontrollpunkte definiert ist, wird die Kurve erst ab dem Parameterwert u=3 bis u=6 gezeichnet. Bei uniformen Knotenwerten sind die Basisfunktionen für jedes parametrische Intervall die selben. |
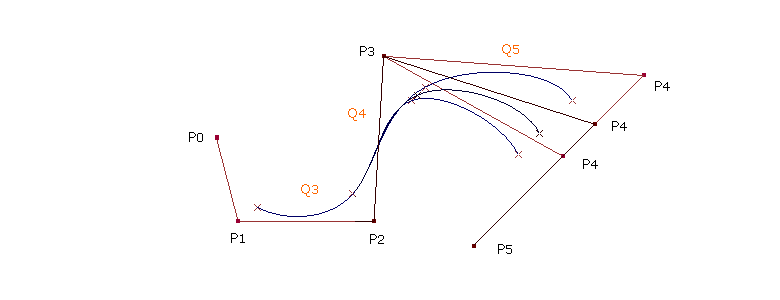 |
| Die Abbildung zeigt die Auswirkungen der Kurve druch eine Veränderung der Position des Kontrollpunktes P4. Der Kurvenabschnitt Q5 wird stark, der Kurvenabschnitt Q4 sehr gering und Q3 wird nicht beeinflusst. Generell beeinfußt ein Kontrollpunkt bei kubischen B-Splines max. Vier Kurvenabschnitt. |
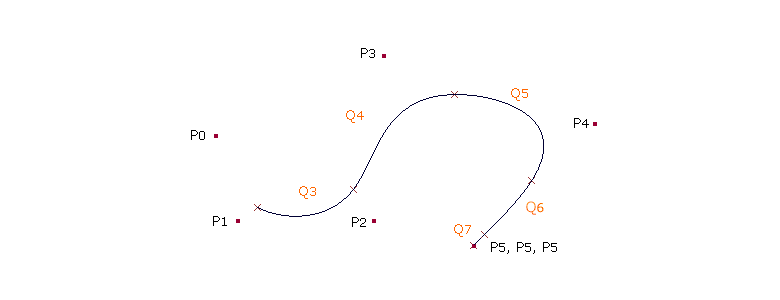 |
| Werden zusätzliche Kontrollpunkte hinzugefügt, schmiegt sich die Kurve näher an die Punkte an. Die Abbildung zeigt die Kurve mit drei Endkontrollpunkten. Durch die zusätzlichen Kurvenabschnitte wird die Kurve bin zum Endpunkt gezeichnet. |
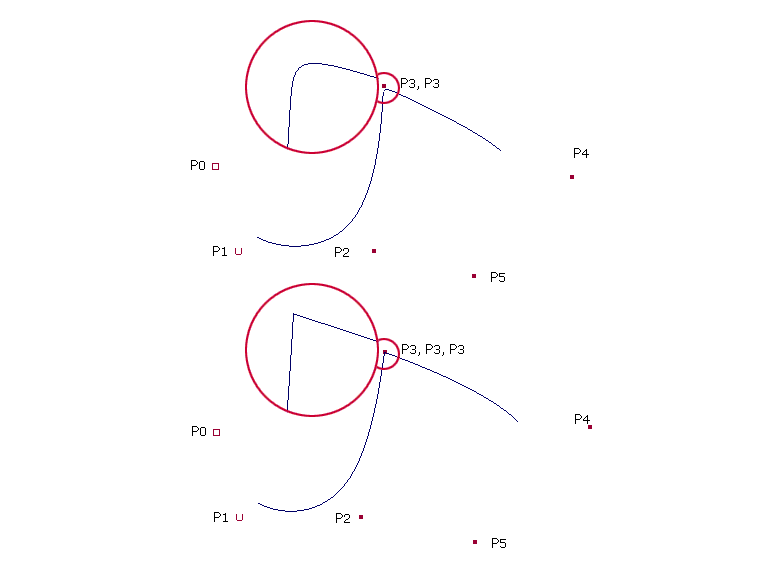 |
| Die Abbildung zeigt die Auswirkung auf die Kurve, wenn innerhalb zusätzliche Kontrollpunkte eingeführt werden: P3 als doppelten Kontrollpunkt: Durch einen zusätzlichen Kontrollpunkt schmiegt sich die Kurve näher an die Kontrollpunkte an. P3 als dreifachen Kontrollpunkt: Werden zwei Kontrollpunkte hinzugefügt, entsteht bei einer kubischen B-Spline eine Ecke. Allgemein gilt: Ein Eckpunkt entsteht, wenn die Anzahl der übereinanderliegenden Kontrollpunkte dem Grad der Kurve entspricht. |
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel