Verlauf
Alle Kapitel anzeigen
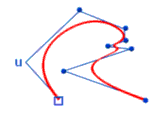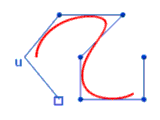
voriges KapitelEigenschaften von B-Splines / Zusammenfassung
Die wichtigsten Eigenschaften der B-Splines:
- B-Splines besitzen n Kontrollpunkte. Eine Kurve wird mit n+1 Gewichtfunktionen beschrieben.
- Die Anzahl der Teilintervalle ist beliebig.
- B-Splines können Polynome mit beliebigen Graden verwenden.
- B-Splines besitzen Modellier-Eigenschaft mit lokaler Kontrolle: Jede Gewichtsfunktion ist über Teilintervalle definiert; daraus resultiert der lokale Einfluss.
- Teilintervalle werden durch Knotenvektoren bestimmt.
- Die Anzahl der Kontrollpunkte kann verändert werden ohne den Grad der Polynome zu verändern.
- Das Einfügen von Knoten und Kontrollpunkten ist eng miteinander verbunden.
- es werden uniforme und nichtuniforme B-Splines unterschieden:
| uniform | nichtuniform |
| Der Abstand zwischen jeweils zwei Knotenwerten ist immer konstant | Beliebige Werte für Knotenwerte und Intervalle sind möglich. |
| periodische Gewichtsfunktionen: alle Gewichtsfunktionen besitzen die gleiche Form und haben jeweils über ein gleich grosses Intervall Einfluss | Die Gewichtsfunktionen besitzen verschieden große Intervalle. Dadurch haben sie unterschiedlichen Einfluss auf die Kurve.td> |
| Mehrfachbestimmungen von Knotenwerten sind nicht möglich | Mehrfachbestimmung von Knotenwerten ist beliebig möglich, führt aber zur Reduzierung der Stetigkeit der Kurve. |
| Beispiel für Knotenvektor: [3,4,5,] | Beispiel für Knotenvektor: [0,1,2,3,3,4,5,] |
