Eine Variable kann man sich als eine Schachtel mit Namen vorstellen, in die bestimmte Inhalte hineingelegt werden können. Wenn man den Namen der Schachtel kennt, kann man später auf deren Inhalt zugreifen.
Variablen bewahren Zustände, Informationen aus der Vergangenheit und Gegenwart, die man in der Zukunft wieder abfragen möchte.
Technischer gesprochen, wird durch eine Variablendefinition (Variablendeklaration) ein bestimmter Speicherplatz im Hauptspeicher reserviert. Über den Variablennamen wird dieser Speicherplatz angesprochen, d.h. man kann den Inhalt abfragen bzw. einen neuen Inhalt hineinschreiben.
Bei der Variablendeklaration wird neben dem Variablennamen auch der Variablentyp festgelegt. Durch den Typ wird festgelegt, wieviel Speicherplatz reserviert werden soll und welche Inhalte in die Schachtel gelegt werden dürfen. Bevor ein Inhalt in die Schachtel gelegt wird (= der Variablen ein Wert zugewiesen wird), wird geprüft, ob der Typ des Inhalts mit dem der Variablen übereinstimmt (= type checking). Wenn das nicht der Fall ist erfolgt eine Fehlermeldung - meist durch den Compiler beim Übersetzen des Programms (= type mismatch error).
Wenn bei einer Variablendeklaration ein Speicherplatz definiert wird, ist dieser nicht "leer", denn die Bits haben auf jeden Fall den Wert 0 oder 1. Nur ist die darin enthaltene Information sinnlos (= undefined). Man muss daher, bevor man das ersten Mal auf den Inhalt der Variablen zugreift, dieser einen Anfangswert zuweisen (= initialisieren).
Die Speicherung eines Inhalt in einer Variablen nennt man Wertzuweisung (assignment).
Eine Wertzuweisung auf eine Varibale hat die allgemeine Gestalt: var = term
wobei zuerst der Term (siehe nächstes Kapitel) auswertet und anschließend das Ergebnis aus einem Zwischenspeicher (Rechenregister) auf den durch die Variable definierten Speicherplatz übertragen wird.
Wichtig: Das Zeichen = ist in diesem Fall der Zuweisungsoperator und nicht das Gleichheitszeichen, das man aus der Schule kennt.
Beispiel in ActionScript:
| var m:Number = 13; |
Das obige Beispiel ist eine Kombination aus Variablendeklaration mit Wertzuweisung (Initialisierung) und könnte auch so geschrieben werden:
| var m:Number; m = 13; |
Über das Schlüsselwort var wird eine Variablendeklaration eingeleitet, gefolgt vom Varaiblennamen und dem Typ: var name:type
Somit wurde ein Speicherplatz unter dem Namen m reserviert, der als Inhalt Zahlen aufnehmen kann.
Im nächsten Schritt wird der Varibalen m der Wert 13 zugewiesen.
Ein Term ist ein sinnvoller Ausdruck aus Zahlen, Variablen, Funktionen, Operatoren und Klammern, der den grammatikalischen Regeln (Syntax) der Programmiersprache entsprechen muss.
Beispiele für Terme:
| 417 | eine Zahl ist ein Term |
| m | eine Variable ist ein Term |
| 43 + 12 | zwei Zahlenterme werden durch den Additionsoperator + verknüpft |
| (a + b) * 2 | die Inhalte der Variblen a und b werden addiert und mit 2 multipliziert |
| sin (alpha) | die Funktion sin wird auf den Inhalt der Variblen alpha angewandt |
Auswertung von Termen:
Ein Term wird immer von innen nach außen ausgewertet und liefert einen Endwert.Im vorigen Kapitel haben wir eine Variable m von Typ Number definiert und ihr den Zahlenwert 13 zugewiesen.
m-1 ist ein Term in dem eine einfache Berechnung durchgeführt wird.
Zuerst wird m ausgewertet und liefert den Wert 13. Die Zahl 1 muss nicht weiter ausgewertet werden.
Anschließend wird vom Wert 13 die Zahl 1 subtrahiert und als Ergebnis liefert der gesamte Term den Wert 12.
Beispiel für die Auswertung eines ActionScript-Terms in dem überprüft wird , ob eine Zahl gerade oder ungerade ist:
Eine gerade Zahl lässt sich ganzzahlig durch 2 dividieren, eine ungerade nicht.
Die Division einer ungeraden Zahl mit 2 ergibt immer eine Dezimalzahl mit ,5.
Nach der Division kann man die größte ganze Zahl kleiner-oder-gleich dem Divisionsergebnis bilden.
Bei einer geraden Ausgangszahl ändert sich im Gegensatz zu einer ungeraden Ausgangszahl dadurch nichts. Damit kann man eine Unterscheidung treffen.
Beispiel:
4 ist gerade. 4:2=2. Die größte ganze Zahl kleiner-oder-gleich 2 ist 2. 2 ist gleich 2
5 ist ungerade. 5:2=2,5. Die größte ganze Zahl kleiner-oder-gleich 2,5 ist 2. 2 ist ungleich 2,5.
| i/2 == Math.floor(i/2) |
Im linken Teilterm wird die Zählvariable i nur durch 2 dividiert, im rechten Teilterm wird auf das Divisionsergebnis noch die Math.floor-Funktion angewandt.
Math.floor(z) liefert die größte ganze Zahl kleiner-oder-gleich der Ausgangszahl z .
Math ist dabei ein ActionScript-Objekt, das mathematische Methoden und Konstanten enthält. Man kann über das Math-Objekt viele bekannte mathematische Funktionen aufrufen.
Mit == kann man zwei Terme auf Gleicheit überprüfen.
Als Ergebnis des Vergleichs wird ein Wert von Typ Boolean geliefert, nämlich true oder false .
Eine Variable vom Typ Boolean kann die Werte true und false annehmen.
Bei einer geraden Zahl sind die beiden Teilterme gleich und der Gesamtterm hat den Wert true, bei einer ungeraden Zahl hat er den Wert false.
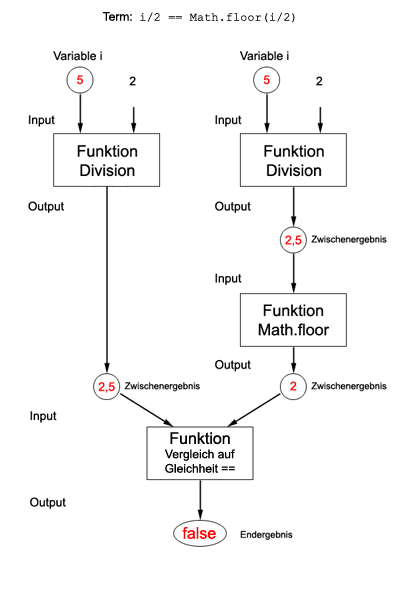
Abb.: Die Auswertung des Terms mit dem Wert 5 für die Variable i liefert den Wert false
Geschachtelte Terme werden immer von innen nach außen ausgewertet.
Ein Array, auch (indiziertes) Feld genannt, kann man sich als eine Reihe von nummerierten Schachteln (Elementen) vorstellen, die unter einem Namen zusammengefasst werden. In diesen Schachtel können Inhalte abgelegt werden. Arrays kommen in fast allen Programmiersprachen vor.
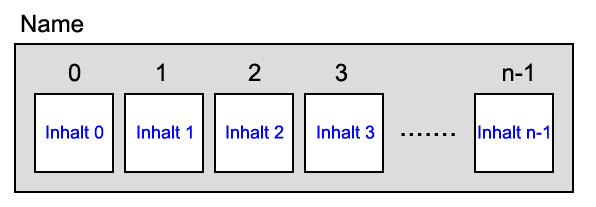
Man beginnt bei der Nummerierung wieder bei 0. D.h. wenn das Array aus n Schachteln (n Elementen) aufgebaut ist, so hat die letzte Schachtel in der Reihe die Nummer (den Index) n-1 .
n ist die Länge (length) des Arrays.
Eine Arraydeklaration in ActionScript hat folgende Gestalt:
| var name = new Array(Inhalt0, Inhalt1, Inhalt2, ...); oder var name = [Inhalt0, Inhalt1, Inhalt2, ...]; |
Die Inhalte können beliebige Ausdrücke (z.B. Zahlen, Zeichenketten, Terme) sein.
Wenn der Inhalt von einem Arrayelement wieder ein Array ist, spricht man von einem geschachtelten Array.
new Array() bzw. [ ] sind Arrays, die keine Elemente enthalten.
Auf den Inhalt der einzelnen Elemente (Schachteln) des Arrays kann man dann über den Arraynamen und die Elementnummer (Index) zugreifen.
| name[Elementnummer] |
In unserem Fall könnte man einen Punkt (u|v) als Array mit zwei Elementen für die x- und y-Koordinate darstellen:
var punkt = new Array(u,v);
punkt[0] liefert die x-Koordinate und punkt[1] die y-Koordinate.
Benannte Arrayelemente
Schöner wäre es jedoch, wenn man "Punkt-x" und "Punkt-y" für die x- und y-Koordinate des Punktes schreiben könnte.
Das ist möglich, wenn man den Arrayelementen einen Namen gibt.
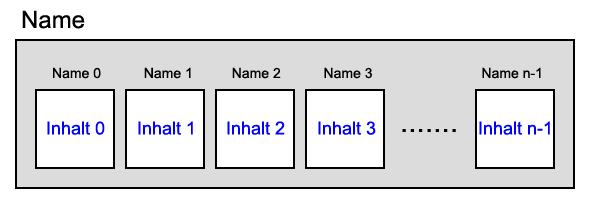
Eine Arraydeklaration hat dann folgende Gestalt:
| var name = new Array(); |
Abgerufen kann der Inhalt eines benannten Elements werden durch
| name.elementname |
Einen Punkt (u|v) als Array mit zwei Elementen für die x- und y-Koordinate könnte man jetzt folgendermaßen darstellen:
var punkt = new Array();
punkt.x = u;
punkt.y = v;
punkt.x liefert dann die x-Koordinate und punkt.y die y-Koordinate.
Eine Sequenz ist eine lineare Abfolge von Anweisungen, die der Prozessor Anweisung für Anweisung abarbeitet.
Die Sequenz ist die einfachste Form, mehrere Anweisungen in einer Abfolge zusammenzufassen.
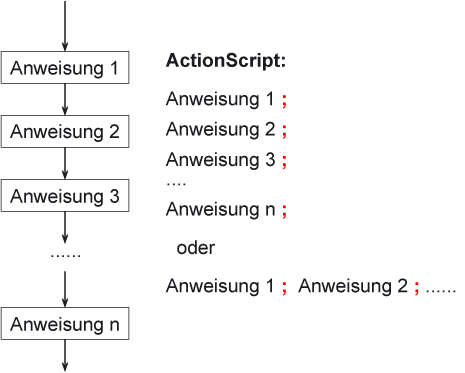
Man muss dem Compiler (siehe Einschub unten) nur mitteilen, wann eine Anweisung endet und eine neue beginnen kann. Im Fall von ActionScript ist das Trennzeichen der Strichpunkt ;
In anderen Programmen beginnt z.B. durch eine neue Programmzeile eine neue Anweisung.
Darstellung einer Sequenz als Struktogramm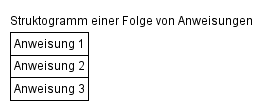

Einschub: Compiler
Der Compiler übersetzt den Programmcode in die Maschinensprache des Prozessores, da dieser den Text nicht "versteht", der in einer höheren Programmiersprache (z.B. ActionScript, Java, C++) geschrieben ist. Prozessoren haben einen eingeschränkten Satz von Befehlen (Befehlssatz), die unmitttelbar Aktionen auf der Hardwareebene bewirken. Wenn der Compiler den Code direkt in die Maschinensprache übersetzt, ist das Ergebnis ein ausführbares (executable) Programm (z.B. in Windows eine exe-Datei), das betriebssystemabhängig ist und von diesem ausgeführt werden kann. Das Betriebssystem kommuniziert mit dem Prozessor.
Ein Compiler kann den Code aber auch auf eine Zwischensprachebene übersetzen, der von einem Player "verstanden" (interpretiert) werden kann. Der Player (z.B. ShockwaveFlash-Player) ist betriebssystemabhängig und übernimmt hier die Kommunikation mit dem Betriebssystem. In diesem Fall sind die vom Compiler erzeugten Dateien, die der Player als Input erhält, betriebssystemunabhängig.
Ein in Flash erstelltes Programm (eine fla-Datei) wird vom Compiler in eine betriebssystemunabhängige ShockwaveFlash-Datei (swf-Datei) übersetzt, die vom betriebssystemabhängigen Flash-Player auf dem jeweiligen System abgespielt werden kann.
Verzweigungen, bedingte Anweisungen
Es ist ein Grundprinzip in der Programmierung wie im täglichen Leben, dass man in Abhängigkeit von bestimmten (Speicher-)Zuständen unterschiedliche Entscheidungen trifft und nachfolgend auf Grund der Entscheidung andere Schritte (Anweisungen) durchführt.
Es gibt daher in jeder Programmiersprache das Konstrukt der bedingten Anweisung.
if-then-else-Anweisung
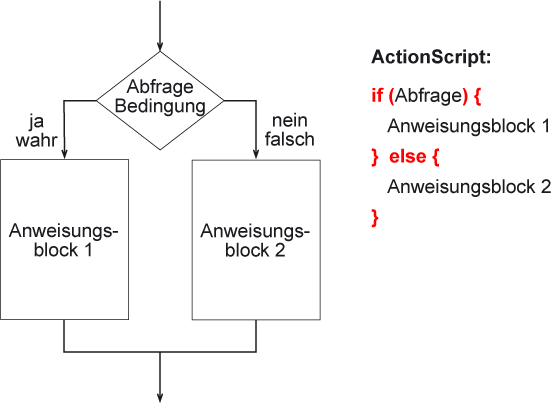
Am Beginn einer if-Anweisung steht immer eine Frage, die mit ja oder nein beantwortet werden kann, oder eine Bedingung, die wahr oder falsch ist.
Wenn (if) die Frage mit Ja beantwortet wird bzw. die Bedingung wahr (true) ist, wird der Anweisungsblock 1 ausgeführt, sonst (else) der Anweisungsblock 2.
Das ist der Grundaufbau einer Entweder-Oder-Entscheidung: if-then-else
Darstellung einer if-then-else-Anweisung als Struktogramm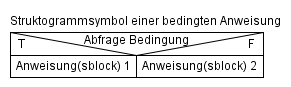
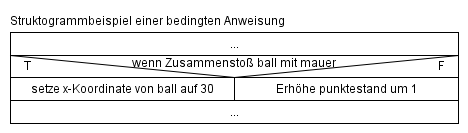
if-then-Anweisung
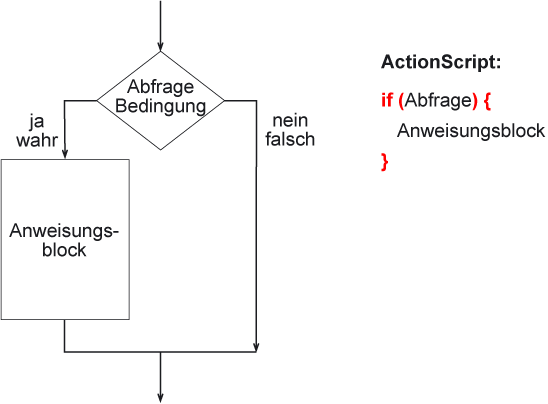
Eine vereinfache Form der if-then-else-Anweisung ist die if-then-Anweisung bei der nur im Fall, dass die Bedingung wahr ist, ein Anweisungsblock aufgeführt wird. Im anderen Fall passiert nichts und der Programmzähler springt zur nächsten Anweisung nach der if-Anweisung.
Darstellung einer if-then-Anweisung als Struktogramm

if-then-else if-Anweisung
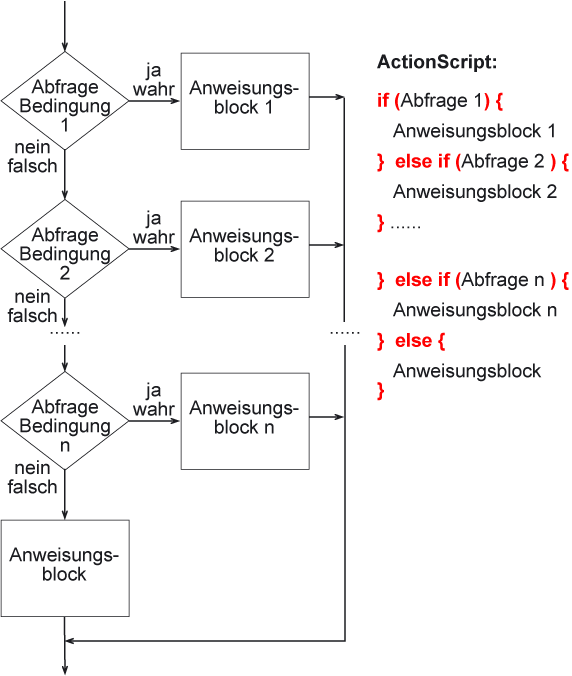
Mehrere immer im else-Zweig geschachtelte if-then-else-Anweisungen können vereinfacht zu einer if-then-else if-Anweisung zusammengefasst werden.
Dabei hat man eine Folge von Bedingungen (Bedingung 1 bis Bedingung n). Wenn die erste Bedingung wahr ist wird der dazugehörige Anweisungblock 1 abgearbeitet. Falls nicht wird die zweite Bedingung geprüft. Falls diese wahr ist wird der zweite Anweisungsblock abgearbeitet. Falls auch die zweite Bedingung falsch ist, wird die dritte abgefragt usw. Wenn keine der Bedingungen wahr ist, wird optional ein abschließender Anweisungsblock ausgewführt.
Darstellung einer geschachtelten if-then-else-Anweisung als Struktogramm

|
if (Bedingung 1){ entspricht if (Bedingung 1){ |
case-Anweisung Fallunterscheidung
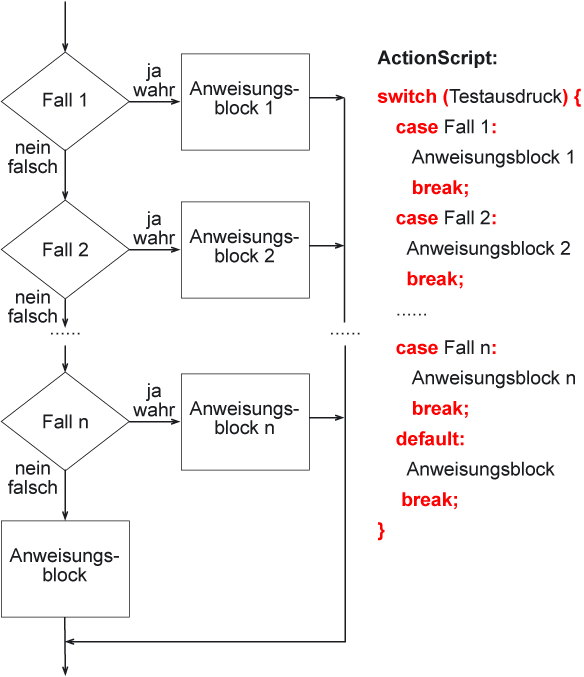
Eine spezielle Form der if-then-else if-Anweisung ist die Fallunterscheidung (switch- oder case-Anweisung).
Bei dieser wird zuerst ein Term festgelegt und anschließend werden möglich Fälle(Zustände) des Terms aufgelistet, bei denen bestimmte Anweisungsblöcke ausgeführt werden sollen.
|
switch (term){ entspricht if (term erfüllt Fall_1){ |
Wenn derselbe Codeabschnitt mehrmals hintereinander wiederholt werden soll, spricht man von einer Schleife.
Ganz allgemein lassen sich Schleife durch nachfolgende Ablaufdiagramme beschreiben:
while-Schleife
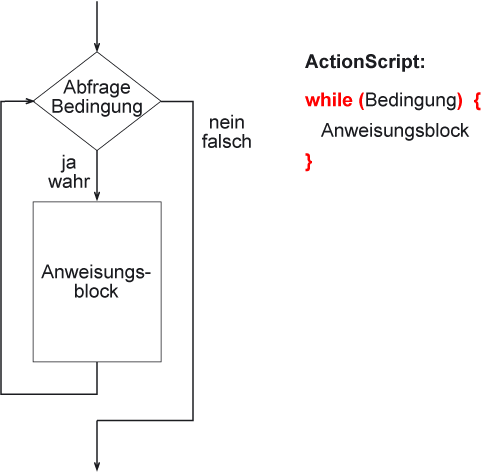
An Beginn einer while-Schleife steht immer eine Frage, die mit ja oder nein beantwortet werden kann, oder eine Bedingung, die wahr oder falsch ist.
Wenn die Frage mit Ja beantwortet wird bzw. die Bedingung wahr ist, wird der nachfolgende Anweisungsblock ausgeführt.
Anschließend wird wieder dieselbe Frage gestellt bzw. der Wahrheitswert der Bedingung abgefragt.
Dieser Vorgang wiederholt sich solange bis die Frage mit Nein beantwortet wird bzw. die Bedingung falsch ist. Man sagt, die Schleife terminiert.
Es ist daher klar, dass sich bei der Abarbeitung des Anweisungsblocks in der Schleife der (Speicher-)Zustand des Programms verändern muss, damit die Bedingung falsch werden kann.
Wenn eine Bedingung nie falsch wird, kommt es zu einer Endlosschleife, in der der Programmablauf hängen bleibt. In der Regel ist das eine unerwünschte Situtation.
Wenn bei einer while-Schleife die Bedingung gleich beim ersten Mal falsch ist, wird der Anweisungblock nie abgearbeitet. Die Anzahl der Wiederholungen sind nicht von Anfang an vorgegeben.
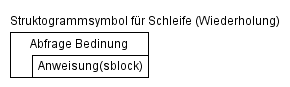

do-while-Schleife (repeat-Schleife)
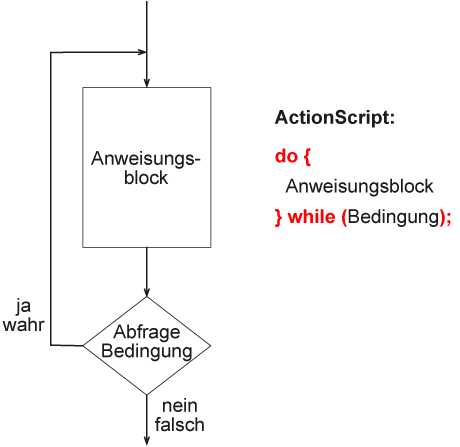
An Beginn einer do-while-Schleife (in anderen Programmiersprachen repeat-Schleife genannt) steht immer ein Anweisungsblock. Nachdem dieser mindestens einmal abgearbeitet wurde folgt eine Frage, die mit ja oder nein beantwortet werden kann, oder eine Bedingung, die wahr oder falsch ist. Wenn die Frage mit Ja beantwortet wird bzw. die Bedingung wahr ist, wird der Anweisungsblock erneut ausgeführt.
Dieser Vorgang wiederholt sich solange bis die Frage mit Nein beantwortet wird bzw. die Bedingung falsch ist. Man sagt, die Schleife terminiert.
Es ist daher klar, dass sich auch bei der Abarbeitung des Anweisungsblocks in der do-while-Schleife der (Speicher-)Zustand des Programms verändern muss, damit die Bedingung falsch werden kann.
Wenn eine Bedingung nie falsch wird, kommt es zu einer Endlosschleife, in der der Programmablauf hängen bleibt. In der Regel ist das eine unerwünschte Situtation.
Bei einer do-while-Schleife wird der Anweisungblock mindestens einmal abgearbeitet. Die Anzahl der Wiederholungen sind nicht von Anfang an vorgegeben.
Darstellung einer repeat-Schleife als Struktogramm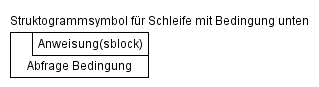
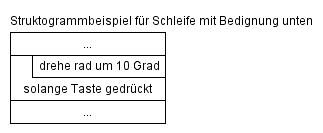
Jede do-while-Schleife lässt sich auch als while-Schleife formulieren:
|
do { entspricht Anweisungsblock; |
for-Schleife (als Spezialfall Zählschleife)
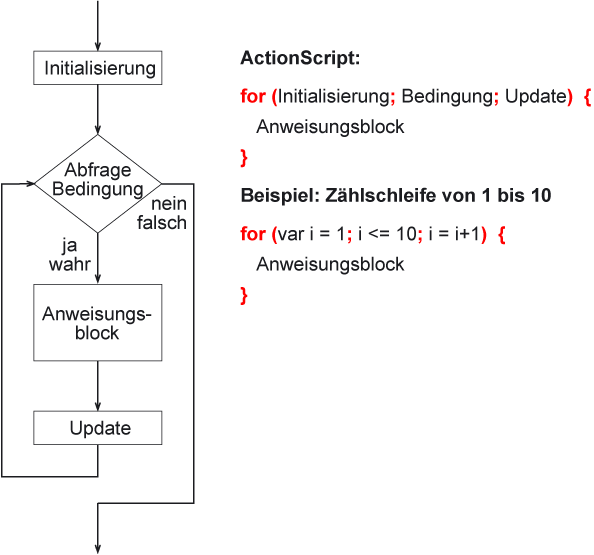
Eine spezielle Schleifenform ist die for-Schleife bei der in der Regel die Anzahl der Wiederholungen von Anfang an feststeht.
Es wird eine (Zähl-)Variable definiert, mit einem Startwert initialisiert. Anschließend definiert man, wie der Inhalt der Variablen in jedem Schleifendurchlauf verändert wird (sehr oft erfolgt ein Zählvorgang nach oben oder unten) und wann dieser (Zähl-)Vorgang beendet wird. In jedem Schleifendurchlauf wird wieder ein Anweisungblock abgearbeitet.
Jede for-Schleife lässt sich auch als while-Schleife formulieren:
|
for (var i= ...; Bedingung mit i; Update von i) { entspricht var i= ...; |
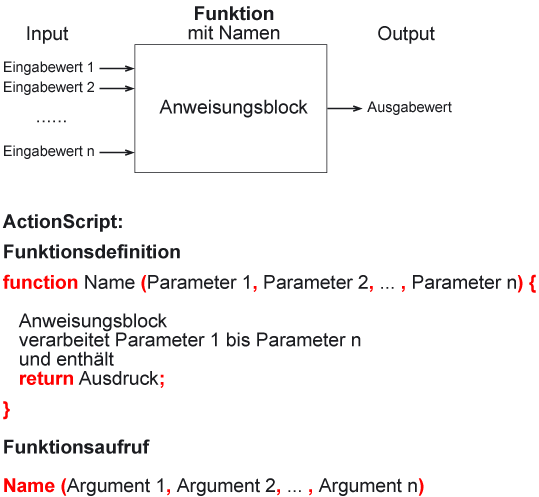
Mittels einer Funktion kann man einen Anweisungsblock zusammenfassen und mit einem Namen versehen (= Funktionsdeklaration).
Unter diesem Namen kann der Programmblock angesprochen und in anderen Anweisungen, ohne den Programmcode immer wieder neu schreiben zu müssen, verwendet werden (= Funktionsaufruf).
In diesem Sinn kann man eine Funktion auch als Abkürzung für einen Programmblock betrachten. Dadurch kann die Lesbarkeit von komplexeren Programmen erhöht werden. Denn eine längere Programmsequenz wird durch einen sprechenden Namen abgekürzt. Man kann sich dadurch vorstellen, was beim Funktionsaufruf passiert und eine detailierte Definition erfolgt später (z.B. weiter unten im Programmcode).
Innerhalb des Anweisungsblocks der Funktion können Variable vorkommen, die vor Beginn der Abarbeitung des Blocks mit konkreten Startwerten belegt sein müssen. Diese Varibalen speichern den Input der Funktion und werden auch als Eingabeparameter bezeichnet. Bei einem Funktionsaufruf werden an diese Eingabeparameter die Startwerte übergeben.
Bei der Abarbeitung des Anweisungsblocks werden diese Eingabewerte verwendet, um bestimmte Anweisungen und Berechnungen durchzuführen.
Als Ergebnis eines Funktionsaufrufs und der dadurch ausgelösten Anweisungen (Berechnungen) kann ein bestimmter (Speicher-)Zustand als Ausgabewert zurückgegeben (= return-Anweisung) werden. Dieser Rückgabewert kann anschließend in einer Varibalen zwischengespeichert oder innerhalb eines Terms weiterverarbeitet werden.
Man sollte immer vor einer Funktionsdeklaration in einem Kommentar die Funktion allgemein beschreiben und die Ein- und Ausgabeparameter, deren Typ und Bedeutung genau angeben.
Es gibt Funktionen, die ohne Input und Output auskommen. Siehe die nachfolgende Funktion fillStage().
Manche Funktionen liefern ohne Input einen Output. Wiederum andere benötigen einen Input, liefern jedoch keinen Output.
Welchen Sinn haben Funktionen, die keinen Output liefern?
Man könnte annehmen, dass Funktionen, die keinen Output liefern, sinnlos sind.
Streng genommen ist das auch so, wenn man eine Funktion als abgeschlossene Input-Output-Maschine betrachtet, die Input erhält, während der Abarbeitung keinen "Kontakt nach außen" hat (keine side-effects) und abschließend den Output zurückliefert.
In vielen Programmiersprachen können jedoch im Anweisungsblock einer Funktion sogenannte globale Variable verändert oder Methoden aufgerufen werden, die zu einer Gesamtzustandsveränderung führen, obwohl die Funktion keinen Rückgabewert liefert. In diesem Fall hat die Ausführung der Funktion side-effects und liefert einen "versteckten" Output.
In der Regel sollte man side-effects vermeiden.
Lässt sich ein Problem mit gegebenen Eingabewerten auf dasselbe Problem mit "kleineren" Eingabewerte reduzieren, kann man die Lösung des Problems rekursiv beschreiben.
Was "kleinere Eingabewerte" bedeutet, muss für das konkrete Problem definiert werden.
Wichtig ist, dass es einen kleinsten Eingabewert gibt, bei man das Problem nicht mehr weiter reduzieren muss. Denn wenn das nicht der Fall ist, kommt man in eine unendliche Rekursion und zu keiner Lösung des Problems.
Beispiel: Wellenlinie
Problem: Wir wollen eine fix vorgegebene Basiskurve n-mal nebeneinander anordnen, wobei an einem vorgegebenen Startpunkt P mit der Zeichnung begonnen wird.
Gegeben sind daher eine natürliche Zahl n für die Anzahl der Wiederholungen und der Startpunkt P.
Gesucht ist eine Funktion f, die die fixe Basiskurve ausgehend vom Startpunkt P n-mal nebeneinander zeichnet.
Das Problem des Zeichnens der Basiskurve von einem vorgegebene Punkt aus wird dabei bereits als gelöst angesehen.
Die Basiskurve hat einen Ausgangspunkt und einen Endpunkt.
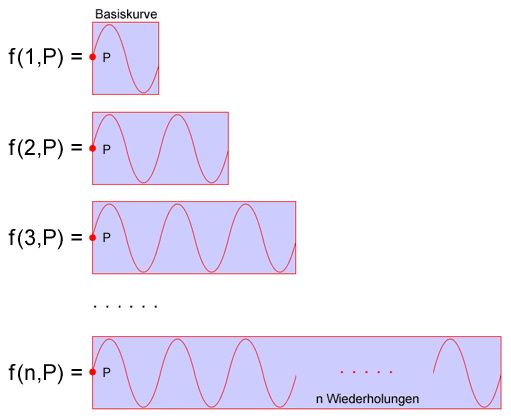
In der obigen Grafik wird schrittweise gezeigt, wie die gesuchte Funktion f für n=1, 2, 3, usw. aussieht. Diese aufzählende Beschreibung lässt sich aber auch wie folgt darstellen:
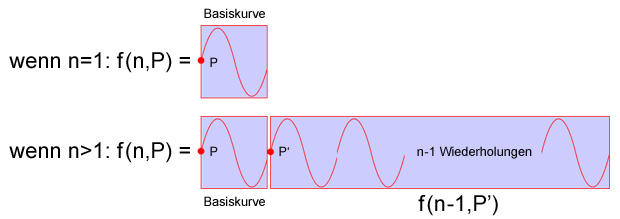
Man erkennt aus der obigen Grafik, dass sich das Problem "die Basiskurve mit n Wiederholungen von P ausgehend zu zeichnen" auf dasselbe "kleinere" Problem reduzieren lässt, bei dem nur mehr "die Basiskurve mit n-1 Wiederholungen von P' ausgehend zu zeichnen" ist. Und zwar nach folgendem Prinzip:
Um "die Basiskurve mit n Wiederholungen von P ausgehend zu zeichnen" genügt es die Basiskurve vom Punkt P ausgehend zu zeichnen und anschließend "die Basiskurve mit n-1 Wiederholungen vom Endpunkt der Basiskurve P' ausgehend zu zeichnen".
Das Problem wurde auf dasselbe kleinere Problem reduziert, von n auf n-1.
Wenn n=1 muss das Problem nicht weiter reduziert werden. In diesem Fall genügt es, die Basiskurve von P ausgehend zu zeichnen.
Diese Beschreibung ist bereits ein Algorithmus wie das Problem zu lösen ist und lässt sich unmittelbar auch in einem ActionScript-Pseudocode formulieren:
| function f (n:Number, P:Point): Void { |
Bemerkung:
Natürlich lässt sich das obige Beispiel sehr einfach als for-Zählschleife realisieren. Aber es ging darum, an diesem einfachen Beispiel das Prinzip der Rekusion zu verdeutlichen.
Grundsätzlich gilt, dass sich jede Schleife als Rekursion darstellen lässt und umgekehrt.
Die Umwandlung einer Schleife in eine Rekusion ist ein triviales Problem. Der umgekehrte Weg, eine Rekursion in Schleifen aufzulösen, ist in der Regel ein nichttriviales Problem, denn Rekursionen können sehr komplex sein.
Viele Probleme lassen sich durch Rekursionen sehr elegant beschreiben und lösen. Bei der Abarbeitung im Computer sind Rekursion jedoch in der Regel langsamer als Schleifen, da der interne Aufwand für Zwischenspeicherungen höher ist.
Ein weiteres, etwas komplexeres Beispiel: Binärer Baum
Problem: Es soll folgende Grafik (ein binärer Baum) gezeichnet werden:
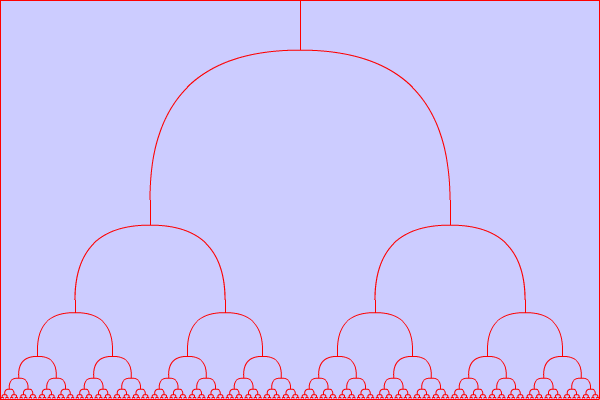
Gegeben sind dabei die Höhe a und Breite b der Basiskurve und ein Startpunkt P von dem ausgehend der binäre Baum gezeichnet wird.
Gesucht ist eine Funktion baum, die die Basiskurve mit Höhe a und Breite b ausgehend vom Startpunkt P zeichnet und an den zwei Endpunkten wieder Basiskurven mit halber Höhe und Breite zeichnet. Das soll solange fortgesetzt werden, bis eine minimale Breite der Basiskurve erreicht ist
Das Problem des Zeichnens der Basiskurve von einem vorgegebene Punkt aus wird dabei bereits als gelöst angesehen.
Die Basiskurve hat einen Ausgangspunkt und zwei Endpunkte.
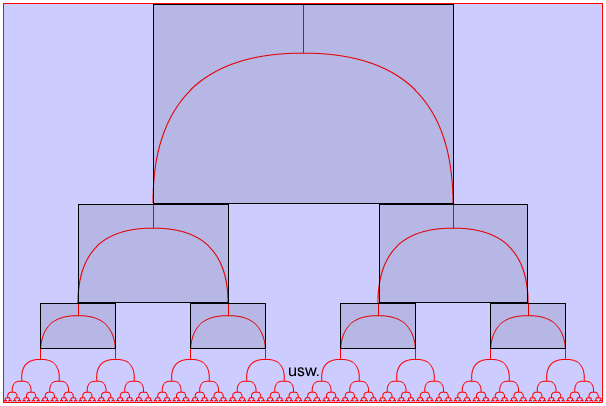
Abb.: Der binäre Baum mit den eingezeichneten, kleiner werdenden Basiskurven.
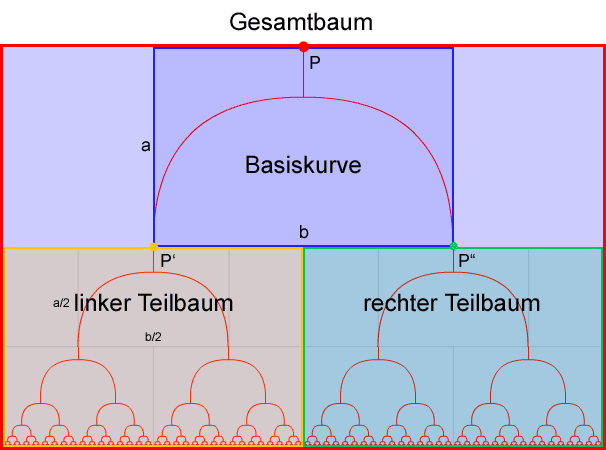
Man erkennt aus der obigen Grafik, dass sich das Problem "ausgehend vom Punkt P einen binären Baum mit einer Startbasiskurve der Höhe a und Breite b zu zeichnen" auf dasselbe "kleinere" Problem reduzieren lässt, bei dem "ausgehend von den Punkten P' und P" zwei binäre Bäume mit Startbasiskurven der Höhe a/2 und Breite b/2 zu zeichnen" sind. Und zwar nach folgendem Prinzip:
Um "ausgehend vom Punkt P einen binären Baum mit einer Startbasiskurve der Höhe a und Breite b zu zeichnen" genügt es die Basiskurve vom Punkt P ausgehend zu zeichnen und anschließend "ausgehend von den Endpunkten der Basiskurve P' und P" zwei binäre Bäume mit Startbasiskurven der Höhe a/2 und Breite b/2 zu zeichnen".
Das Problem wurde auf dasselbe kleinere Problem reduziert, von a auf a/2 (bzw. von b auf b/2).
Wenn a (bzw. b) unter einem fixen Grenzwert liegt, muss das Problem nicht weiter reduziert werden. In diesem Fall wird nichts mehr gezeichnet.
Diese Beschreibung ist wieder ein Algorithmus wie das Problem zu lösen ist und lässt sich unmittelbar auch in einem ActionScript-Pseudocode formulieren:
| function baum (P:Point, a:Number, b:Number): Void { |
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen