Verlauf
Alle Kapitel anzeigen
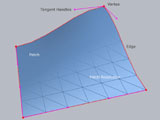
voriges KapitelEigenschaften von Bézier-Kurvensegmenten / Zusammenfassung
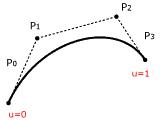
- Eine Bézier-Kurve ist ein Polynom. Der Grad des Polynoms ist immer um eins niedriger als die Anzahl der Kontrollpunkte. Bei kubischen Bézier-Kurven handelt es sich um Polynome dritten Grades mit 4 Kuntrollpunkte.
- In den den meisten 3d und 2d Computerprogrammen werden kubischen Polynomen verwendet.
- Die Kontrollpunkte üben einen "globalen" Einfluß aus. Das Bewegen eines jeden Kontrollpunktes betrifft das ganze Kurvensegment.
- Der erste und der letzte Kontrollunkt sind die Endpunkte des Kurvenabschnitts = Kurvenpunkte.
- Das bewegen der Kontrollpunkte verändert die Länge und Richtung der Tangentenvektoren.
- Die Kurve wird transformiert, in dem beliebige affine Transformationen (also jede Kombination linearer Transformationen) auf die Kontrollpunkte angewendet werden.
- Komplexe Kurven werden aus kubischen Bézier-Kurvensegmente zusammengesetzt.
