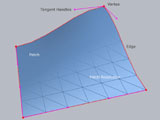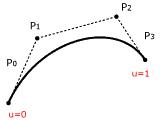
Im Falle der Bézier-Kurven sind die Basisfunktionen die Bernsteinschen kubischen Polynome:
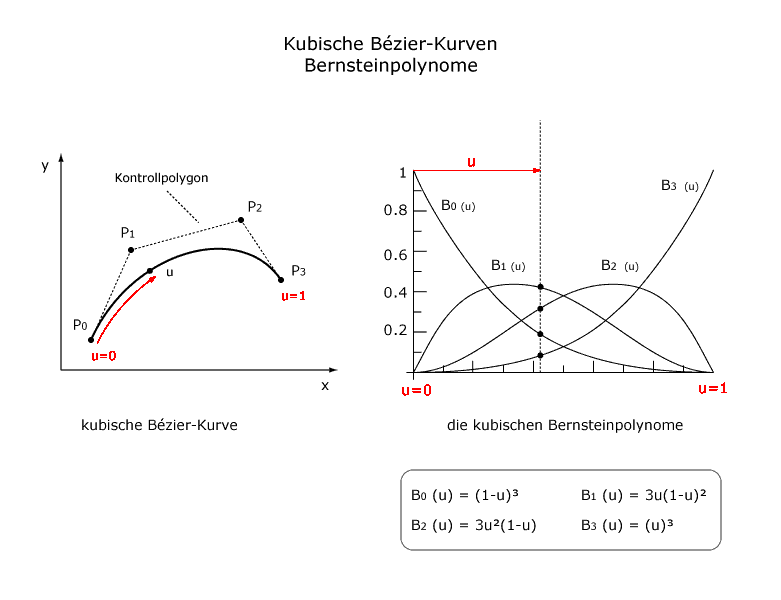 |
| Die Abbildung zeigt rechts die kubischen Bernsteinpolynome und links eine Bézier-Kurve. Wird eine Bézier-Kurve vom Anfangspunkt P0 (u= 0) zum Endpunkt P3 (u=1) verfolgt, entspricht das dem Bewegen einer vertikalen Geraden durch die Basisfunktionen (siehe Abbildung rechts). Die Schnittpunkte dieser Geraden mit den Basisfunktionen ergeben die Werte von den Bernsteinpolynomen für den entsprechenden Punkt auf der Kurve. Die Gewichtung jeder Basisfunktion durch die Kontrollpunkte P0, P1, P2 und P3 ermittelt den entsprechenden Punkt der Kurve im Raum. Das Verbinden der vier Kontrollpunkte ergibt das so genannte Kontrollpolygon. Das Verschieben eines Kontrollpunktes führt zu einer Veränderung der Kurve. |
mehr Informationen zu Polynomiale Kurven und Bézier-Kurven: 3d-Computergrafik / Allen Watt; Computergrafik / Michael Bender, Manfred Brill
Bücher / 3d-Computergrafik / Allgemein
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel