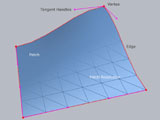
Klassische Kurvenlineal versus mathematische Darstellung frei formbarer Oberflächen
Die geschichtliche Entwicklung der Bézier-Kurven beginnt in den späten 50er Jahren in der Autoindustrie. Vor der Entwicklung der Bézier-Kurven zeichneten die Designer Kurven am Papier durch Kurvenlineale. Ausgehend von den Skizzen wurden in zeitaufwendigen Prozessen maßstäbliche Modelle aus Holz und Ton gefertigt. Ein finales Master-Modell aus Gips wurde schließlich für die Kopiermaschinen eingesetzt. Das primäre Ziel war die Darstellung frei geformter Kurven und Oberflächen zu ermöglichen um den Designprozess in der Automobilindustrie zu optimieren:
Seit 1955 wurden die ersten sog. NC(Numerical Control)-Maschinen entwickelt und eingesetzt. Diese konnten geometrische Daten aus einem Rechner interpretieren und auf Werkzeuge übertragen. Paul de Casteljau, der bei Citroen tätig war, entwickelte 1959 ein einfaches und schnell berechenbares Konstruktionsprinzip für Kurven und gekrümmte Oberflächen. Parallel entdekte ein anderer Ingenieur - Pierre Bézier, der für Renault arbeitete, 1962 unabhängig von De Casteljau dieselbe Formel. Es folgte ein Rechtsstreit, der durch einen Vergleich beigelegt wurde: Die allgemeine Formel und damit die Kurven wird folglich nach Pierre Bézier benannt (Bernstein-Bézier-Polynom, Bézier-Kurve/Fläche) und das zugrunde liegende Konstruktionsprinzip wird nach De Casteljau (De Casteljau-Algorithmus) benannt. Die Entwicklungen von Bézier und Casteljau werden als Grundlage für ein CAD-Programm benutzt. Bereits wenige Jahre später konnte die Bézier-Kurven unmittelbar zur Steuerung von NC-Fräsen herangezogen werden. Die Entwicklung von Bézier und de Casteljau gaben Anstoß zu parallelen Weiterentwicklungen in anderen Industriebereichen wie Schiffsbau und Luftfahrt.
Konzept der Bézier-Kurvendarstellung:
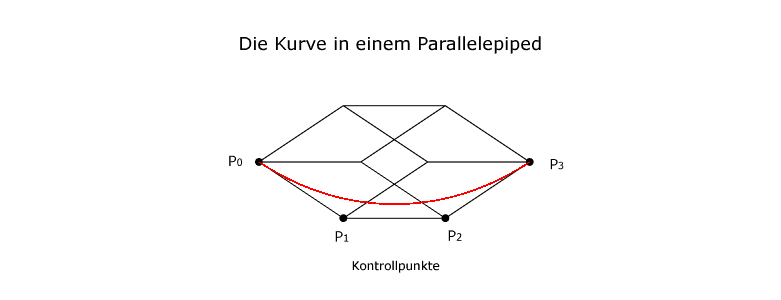 |
| Die Kurvendarstellung sollte geometrisch begründbar und die zugrunde liegende Mathematik leicht verständlich sein. Béziers Grundidee war eine Kurve durch ein Parallelepiped (6 deckungsgleiche Parallelogramme, die in parallelen Ebenen zueinander liegen) zu definieren. Die Kurve konnte vollständig durch vier Punkte, P1, P2, P3, P4 - bekannt als Kontrollpunkte - festgelegt werden. |
In der 3d-Computergrafik werden Kurven durch mathematisch definierte Kurven beschrieben. Dafür eignet sich das Heranziehen von Polynomen. Das Erscheinungsbild und die Handhabung der Kurve ist entscheidend vom Grad der Polynome abhängig. Der Grad des Polynoms ist immer um eins niedriger als die Anzahl der Kontrollpunkte.
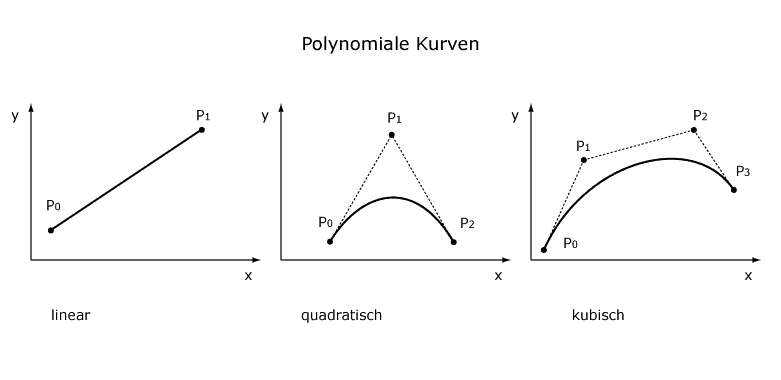 |
| Lineare Polynome: |
Im Falle der Bézier-Kurven sind die Basisfunktionen die Bernsteinschen kubischen Polynome:
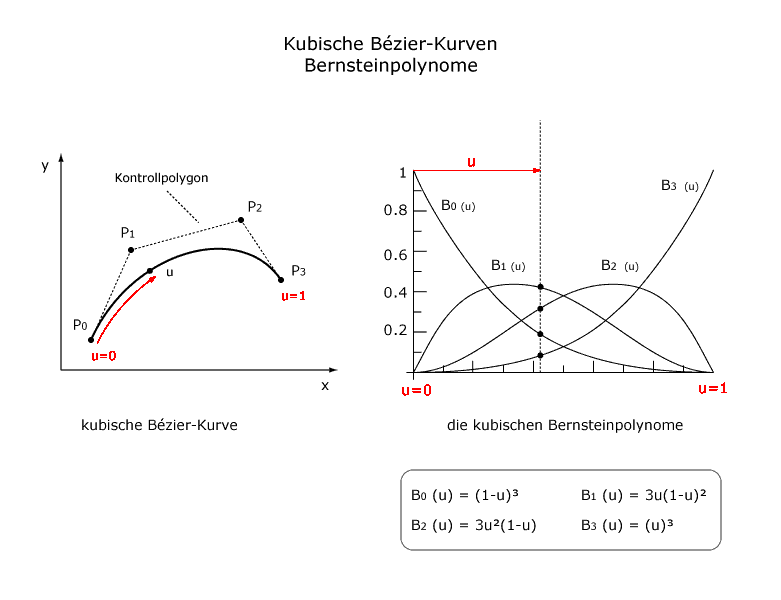 |
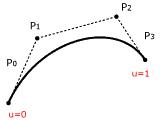
| Die Abbildung zeigt rechts die kubischen Bernsteinpolynome und links eine Bézier-Kurve. Wird eine Bézier-Kurve vom Anfangspunkt P0 (u= 0) zum Endpunkt P3 (u=1) verfolgt, entspricht das dem Bewegen einer vertikalen Geraden durch die Basisfunktionen (siehe Abbildung rechts). Die Schnittpunkte dieser Geraden mit den Basisfunktionen ergeben die Werte von den Bernsteinpolynomen für den entsprechenden Punkt auf der Kurve. Die Gewichtung jeder Basisfunktion durch die Kontrollpunkte P0, P1, P2 und P3 ermittelt den entsprechenden Punkt der Kurve im Raum. Das Verbinden der vier Kontrollpunkte ergibt das so genannte Kontrollpolygon. Das Verschieben eines Kontrollpunktes führt zu einer Veränderung der Kurve. |
mehr Informationen zu Polynomiale Kurven und Bézier-Kurven: 3d-Computergrafik / Allen Watt; Computergrafik / Michael Bender, Manfred Brill
Bücher / 3d-Computergrafik / Allgemein
Der Algorithmus von de Casteljau gilt als die erste Lösung, mathematisch definierte Kurven im Computer einfach und schnell zu berechnen. Durch den Algorithmus kann jeder Kurvenpunkt eines Bézier-Kurvensegments rekursiv berechnet werden. Der Algorythmus basiert auf der Rekursionseigenschaft der Bernstein-Polynome. Das Ergebnis ist keine stetige Kurve, sondern eine Menge von Geraden.
mehr Informationen zu de Casteljau-Algorithmus: 3d-Computergrafik / Allen Watt, Computergrafik / Michael Bender, Manfred Brill
Bücher / 3d-Computergrafik / Allgemein
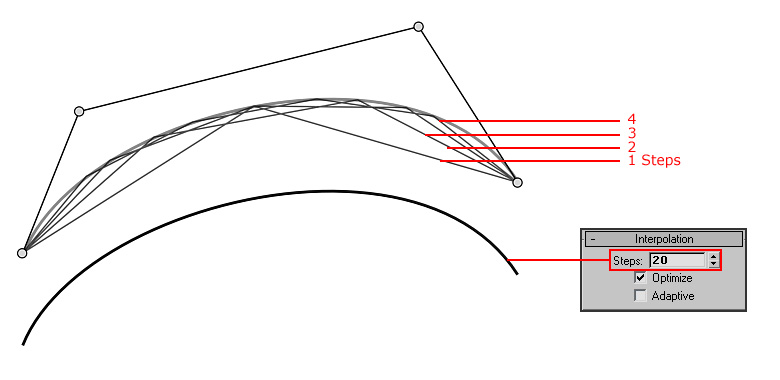 |
| Eine Annäherung an eine Bézierkurve durch Casteljau-Algorithmus am Beispiel 3dsmax: |
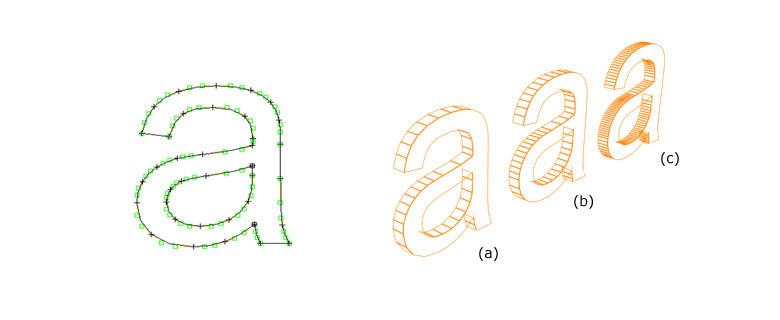 |
| Unterschiedliche Bézier-Interpolation am Beispiel einer Schriftart in 3ds max: |
Bézier-Kurvensegmente verbinden
Für das Verbinden von kubischen Bézier-Kurvenabschnitten gelten folgende Bedingungen:
- Stetigkeit der Position
bedeutet, dass der Endpunkt des ersten Kurvenabschnittes mit dem Anfangspunkt des zweiten übereinstimmt. - Stetigkeit erster Ordnung oder tangentiale Stetigkeit
bedeutet, dass der vorletzte Punkt (S2) und der Endpunkt (S3) des ersten Kurvenabschnittes mit dem Anfangspunkt (R0) und dem zweiten Kurvenpunkt (R1) des zweiten Kurvenabschnittes auf einer Geraden liegen.
Die Standardbedingung ist die der Stetigkeit der Position. Der Unterschied zwischen der Stetigkeit der Position und der Stetigkeit erster Ordnung für Bézier-Kurven wir in der folgenden Abbildung gezeigt:
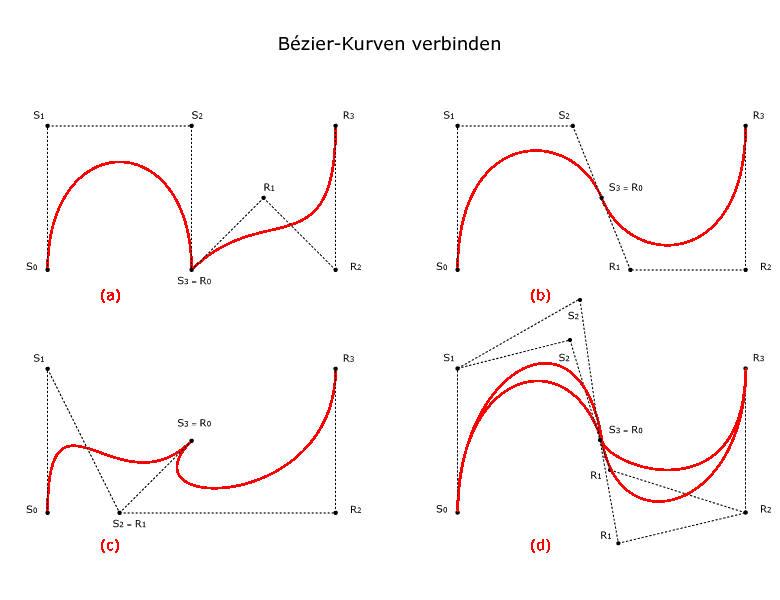 |
| Stetigkeit zwischen Bézier-Kurvenabschnitte: (a) Stetigkeit der Position zwischen Bézier-Punkten: S3= R0 (b) Tangentiale Stetigkeit zwischen Bézier-Punkten; (c) Weiteres Beispiel für Stetigkeit der Position zwischen Bézier-Punkten: S3= R0, S2= R1 (d) Weiteres Beispiel für tangentiale Stetigkeit zwischen Bézier-Punkten: S2,S3,R0 und R1 liegen auf einer Geraden. Die Abstände zwischen S2-S3 und R0-R1 sind ungleich. |
Komplexe Bézier-Kurven am Beispiel 3ds max.
 |
| Beispiel für Bézier-Kurven in 3ds: Corner (Ecke): Wird ein Kurvenpunkt (rotes Kreuz) zu einer Ecke umgewandelt, stehen keine Kontrollpunkte (grünes Quadrat) zur Verfügung. Smooth (Glatt): Wir ein Kurvenpunkt "Smooth" eingestellt, stehen keine Kontrollpunkte zur Verfügung. Es wird eine glatte, kontinuierliche Kurven erstellt. Die Krümmung an einem glatten Kurvenpunkt wird vom Abstand der angrenzenden Kontrollpunkte festgelegt. Bézier: Ein Kurvenpunkt mit gesperrten, kontinuierlichen Tangenten-Haltepunkten (Kontrollpunkte) . Es wird eine glatte, kontinuierliche Kurven erstellt. Die Krümmung am Kurvenpunkt wird von der Richtung und Länge der Tangenten-Haltepunkte (Kontrollpunkte) bestimmt. Bezier-Corner (Bezier-Ecke): Kurvenpunkte mit diskontinuierlichen Tangenten-Haltepunkten, die eine scharfe Ecke bilden. Die Krümmung des Segments nach der Ecke wird von der Richtung und Länge der Tangenten-Haltepunkte bestimmt. |
Eigenschaften von Bézier-Kurvensegmenten / Zusammenfassung
- Eine Bézier-Kurve ist ein Polynom. Der Grad des Polynoms ist immer um eins niedriger als die Anzahl der Kontrollpunkte. Bei kubischen Bézier-Kurven handelt es sich um Polynome dritten Grades mit 4 Kuntrollpunkte.
- In den den meisten 3d und 2d Computerprogrammen werden kubischen Polynomen verwendet.
- Die Kontrollpunkte üben einen "globalen" Einfluß aus. Das Bewegen eines jeden Kontrollpunktes betrifft das ganze Kurvensegment.
- Der erste und der letzte Kontrollunkt sind die Endpunkte des Kurvenabschnitts = Kurvenpunkte.
- Das bewegen der Kontrollpunkte verändert die Länge und Richtung der Tangentenvektoren.
- Die Kurve wird transformiert, in dem beliebige affine Transformationen (also jede Kombination linearer Transformationen) auf die Kontrollpunkte angewendet werden.
- Komplexe Kurven werden aus kubischen Bézier-Kurvensegmente zusammengesetzt.
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen