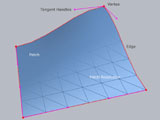
Klassische Kurvenlineal versus mathematische Darstellung frei formbarer Oberflächen
Die geschichtliche Entwicklung der Bézier-Kurven beginnt in den späten 50er Jahren in der Autoindustrie. Vor der Entwicklung der Bézier-Kurven zeichneten die Designer Kurven am Papier durch Kurvenlineale. Ausgehend von den Skizzen wurden in zeitaufwendigen Prozessen maßstäbliche Modelle aus Holz und Ton gefertigt. Ein finales Master-Modell aus Gips wurde schließlich für die Kopiermaschinen eingesetzt. Das primäre Ziel war die Darstellung frei geformter Kurven und Oberflächen zu ermöglichen um den Designprozess in der Automobilindustrie zu optimieren:
Seit 1955 wurden die ersten sog. NC(Numerical Control)-Maschinen entwickelt und eingesetzt. Diese konnten geometrische Daten aus einem Rechner interpretieren und auf Werkzeuge übertragen. Paul de Casteljau, der bei Citroen tätig war, entwickelte 1959 ein einfaches und schnell berechenbares Konstruktionsprinzip für Kurven und gekrümmte Oberflächen. Parallel entdekte ein anderer Ingenieur - Pierre Bézier, der für Renault arbeitete, 1962 unabhängig von De Casteljau dieselbe Formel. Es folgte ein Rechtsstreit, der durch einen Vergleich beigelegt wurde: Die allgemeine Formel und damit die Kurven wird folglich nach Pierre Bézier benannt (Bernstein-Bézier-Polynom, Bézier-Kurve/Fläche) und das zugrunde liegende Konstruktionsprinzip wird nach De Casteljau (De Casteljau-Algorithmus) benannt. Die Entwicklungen von Bézier und Casteljau werden als Grundlage für ein CAD-Programm benutzt. Bereits wenige Jahre später konnte die Bézier-Kurven unmittelbar zur Steuerung von NC-Fräsen herangezogen werden. Die Entwicklung von Bézier und de Casteljau gaben Anstoß zu parallelen Weiterentwicklungen in anderen Industriebereichen wie Schiffsbau und Luftfahrt.
Konzept der Bézier-Kurvendarstellung:
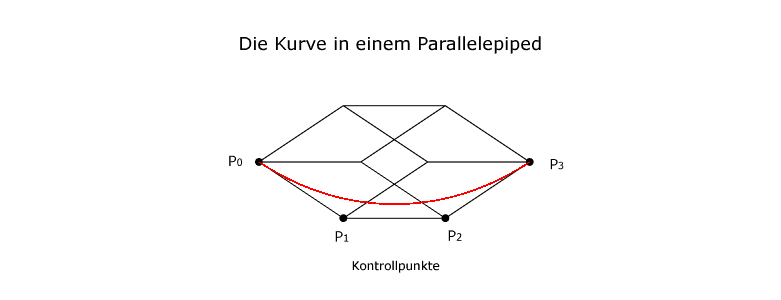 |
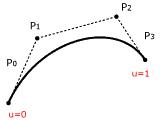
| Die Kurvendarstellung sollte geometrisch begründbar und die zugrunde liegende Mathematik leicht verständlich sein. Béziers Grundidee war eine Kurve durch ein Parallelepiped (6 deckungsgleiche Parallelogramme, die in parallelen Ebenen zueinander liegen) zu definieren. Die Kurve konnte vollständig durch vier Punkte, P1, P2, P3, P4 - bekannt als Kontrollpunkte - festgelegt werden. |
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen