Bézier-Kurven

 
erstellt von: Jürgen Hagler
erstellt am: 28.07.2005 geändert am: 02.10.2006 Modul-ID: 13079
Zu den Favoriten Modul bearbeiten Download des Moduls
Keywords
voriges Kapitel nächstes Kapitel

Der de Casteljau-Algorithmus

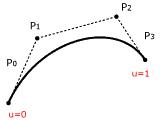
Der Algorithmus von de Casteljau gilt als die erste Lösung, mathematisch definierte Kurven im Computer einfach und schnell zu berechnen. Durch den Algorithmus kann jeder Kurvenpunkt eines Bézier-Kurvensegments rekursiv berechnet werden. Der Algorythmus basiert auf der Rekursionseigenschaft der Bernstein-Polynome. Das Ergebnis ist keine stetige Kurve, sondern eine Menge von Geraden.

mehr Informationen zu de Casteljau-Algorithmus: 3d-Computergrafik / Allen Watt, Computergrafik / Michael Bender, Manfred Brill
Bücher / 3d-Computergrafik / Allgemein

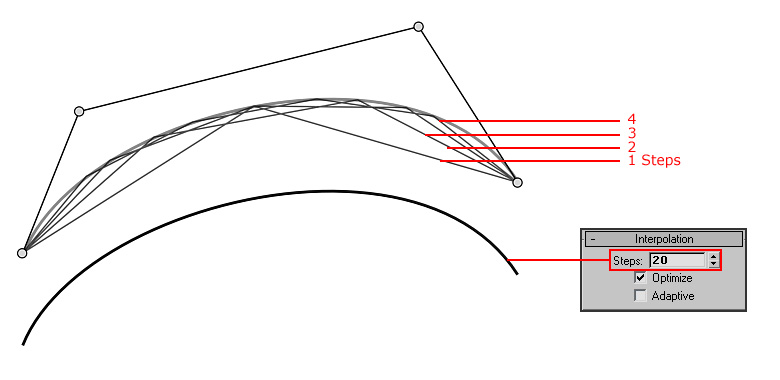Eine Annäherung an eine Bézierkurve durch Casteljau-Algorithmus am Beispiel 3dsmax:
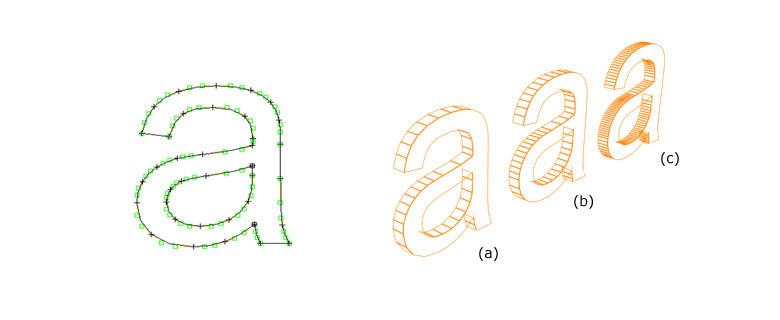In der Kategorie „Interpolation“ einer Bézier-Kurve in 3dsmax wird bestimmt, wie das Programm die Kurve berechnet. Die Kurven sind in kleine, gerade Linien unterteilt, die sich der mathematisch definierten Kurve annähern. Die Anzahl der Unterteilungen zwischen Scheitelpunkten auf dem Spline wird Steps (Schritte) genannt. Je mehr Interpolationsschritte verwendet werden, desto glatter wird die Kurve angezeigt bzw. berechnet. Werden aus Bézier-Kurven z. B. Polygonflächen generiert, gibt die Bézier-Kurveninterpolation auch die Auflösung der Geometrie an.

Unterschiedliche Bézier-Interpolation am Beispiel einer Schriftart in 3ds max:
(a) Interpolation Steps: 1
(b) Interpolation Steps: 2
(c) Interpolation Steps: 6 (Standardeinstellung)
voriges Kapitel nächstes Kapitel

Ergänzende und vertiefende Module

erstellt von: Thomas Maier erstellt am: 20.09.2004 geändert am: 10.04.2006

erstellt von: Werner Pötzelberger erstellt am: 07.03.2005 geändert am: 10.04.2006