In der 3d-Computergrafik hat sich neben der Bézier-Kurven die Nurbs-Kurve als Standard etabliert. Viele 3d-Programme bieten sowohl Bézier-, als auch Nurbs-Kurven. Dieses Kapitel behandelt uniforme und nichtuniforme B-Splines, die die Basis für die Nurbs-Kurven darstellen.
Geschichtliches
Spline: (engl.) übersetzt: das Kurvenlineal, ein längliches, dünnes Stück Holz oder Metall;
Geschichtlich gesehen gingen die B-Splines (Basis-Splines) den Bézier-Kurven voraus. Entwickelt wurden die B-Splines noch vor der Computermodellierung im Schiffsbau, wo die Designer lebensgroße Kurven zeichnen mussten. Für Zeichnungen im kleineren Maßstab verwendeten die Konstrukteure vorgefertigte Kurvenlineale. Für maßstäbliche Pläne war diese Methode jedoch ungeeignet. Die Zeichner verwendeten dafür lange, dünne Metallstreifen. Diese Streifen, auch Splines genannt, wurden in die gewünschte Form geschoben. Mit Bleigewichten, so genannte Knots, wurde die Form der Streifen fixiert. Die Fixierung bzw. Formgebung erfolgt durch "Gewichte", daher auch der Name "Gewichtsfunktionen".
Vergleich B-Splines / Bézier-Kurven
Die entscheidenden Vor- bzw. Nachteile von B-Splines gegenüber Bézier-Splines:
| B-Splines | Bézier-Kurven |
| Der Grad der Polynome ist unabhängig von der Anzahl der Kontrollpunkte. | Bei Bézier-Kurvensegmenten ist der Grad des Polynoms immer um eins niedriger als die Anzahl der Kontrollpunkte. Bei kubischen Bézier-Kurvensegmenten handelt es sich um Polynome dritten Grades mit vier Kontrollpunkten. |
| Bei B-Splines ist eine lokale Kontrolle der Kurve möglich. | Die Kontrollpunkte üben einen "globalen" Einfluss auf das Kurvensegment aus. Das Bewegen eines jeden Kontrollpunktes betrifft das ganze Kurvensegment. |
| Kontrollpunkte können beliebig verschoben werden. | Zur Bewahrung der Stetigkeit von Bézier-Kurvensegmenten ist das Bewegen von Kontrollpunkten gewissen Bedingungen unterworfen (siehe Bézier-Kurvensegmente verbinden). |
| Der de Boor-Algorithmus liefert die Auswertung der Kurve | Der Casteljau-Algorithmus liefert die Auswertung der Kurve. |
Die Art von B-Splines hängt von dem verwendeten Knotenvektor ab. Der Knotenvektor ergibt sich aus den Knotenintervallen bzw. Knotenwerten. B-Splines unterscheiden sich dadurch, dass die Knotenintervalle der einzelnen Knotenwerte entweder gleich groß sind oder variieren:
- uniforme (periodische) B-Splines
- offene uniforme B-Splines
- nicht-uniforme B-Splines
Da in der Computergrafik in der Regel kubische Nurbs-Kurven eingsetzt werden, beschränken sich die weiteren Erklärungen auf kubische B-Splines.
Ein B-Spline besteht generell aus Teilen von Polynomen, die zu einer gesamten Kurve zusammengestellt werden. Die Anzahl von Kurvenabschnitten (Spans) ist beliebig. Folglich können auch beliebig viele Kurvenpunkte eingefügt werden. Bei einer kubischen B-Spline ist jeder Kurvenabschnitt durch vier Basisfunktionen und vier Kontrollpunkte definiert. die Kontrollpunkte der B-Splines haben einen sogenannten Knotenwert (u-Parameter). Diese u-Parametrisierung erstreckt sich vom Anfangspunkt bis zum Endpunkt der Kurve. Jeder Kurvenabschnitt besitzt am Anfang und am Ende einen Knotenwert. Der Verbindungspunkt beim Wert von u zwischen den Segmenten wird als Knotenwert bezeichnet.
Bei uniformen B-Splines ist der Abstand zwischen zwei Knotenwerten immer konstant. Die Gewichtsfunktionen einer uniformen B-Spline sind periodisch und folglich einfacher zu berechnen. Solche B-Splines werden als uniforme bzw. periodische B-Splines bezeichnet.
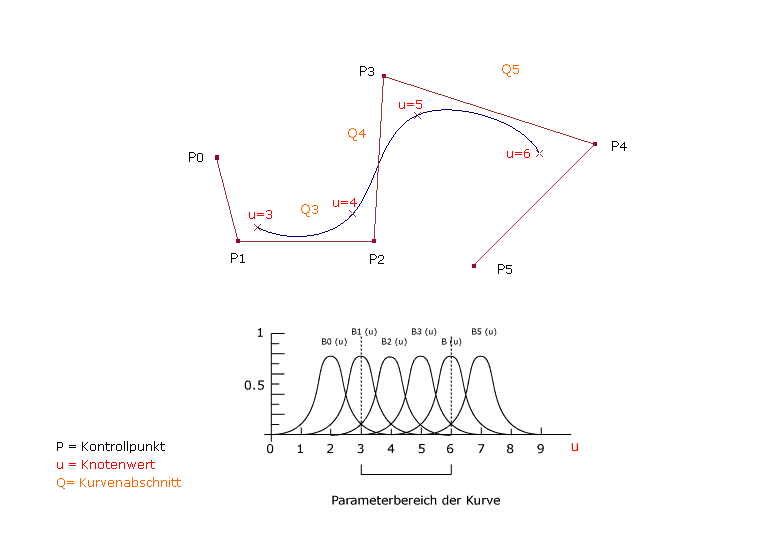 |
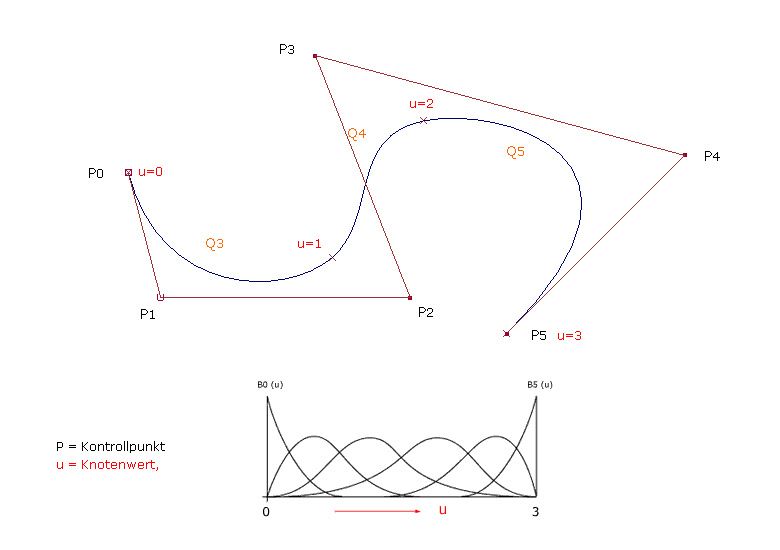
| Die Abbildung zeigt eine uniforme B-Spline-Kurve dritten Grades, die durch die Position von sechs Kontrollpunkten definiert ist. Jeder Kurvenabschnitt (Q) ist durch vier Kontrollpunkte beeinflusst. Da jeder Kurvenabschnitt durch vier Kontrollpunkte definiert ist, wird die Kurve erst ab dem Parameterwert u=3 bis u=6 gezeichnet. Bei uniformen Knotenwerten sind die Basisfunktionen für jedes parametrische Intervall die selben. |
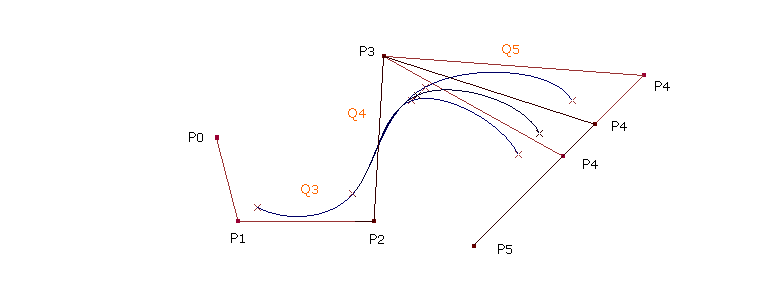 |
| Die Abbildung zeigt die Auswirkungen der Kurve druch eine Veränderung der Position des Kontrollpunktes P4. Der Kurvenabschnitt Q5 wird stark, der Kurvenabschnitt Q4 sehr gering und Q3 wird nicht beeinflusst. Generell beeinfußt ein Kontrollpunkt bei kubischen B-Splines max. Vier Kurvenabschnitt. |
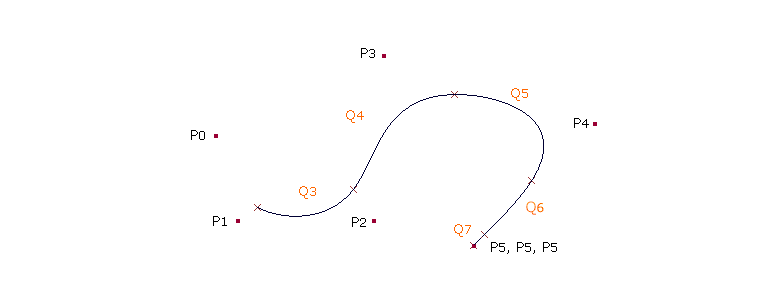 |
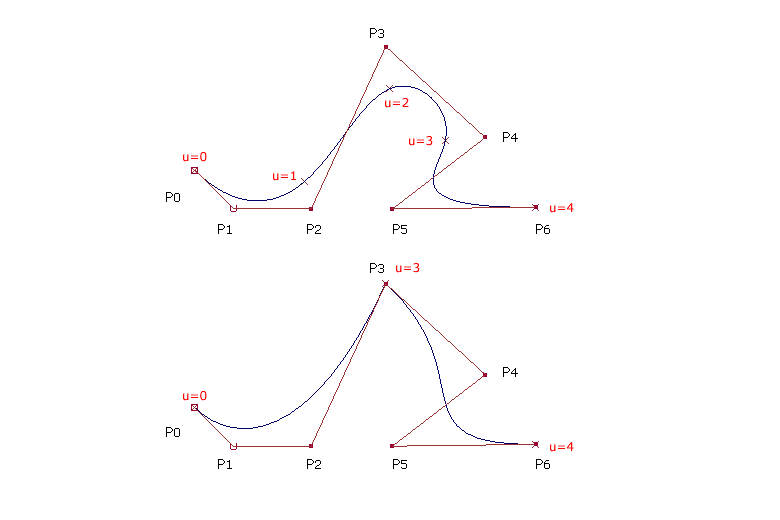
| Werden zusätzliche Kontrollpunkte hinzugefügt, schmiegt sich die Kurve näher an die Punkte an. Die Abbildung zeigt die Kurve mit drei Endkontrollpunkten. Durch die zusätzlichen Kurvenabschnitte wird die Kurve bin zum Endpunkt gezeichnet. |
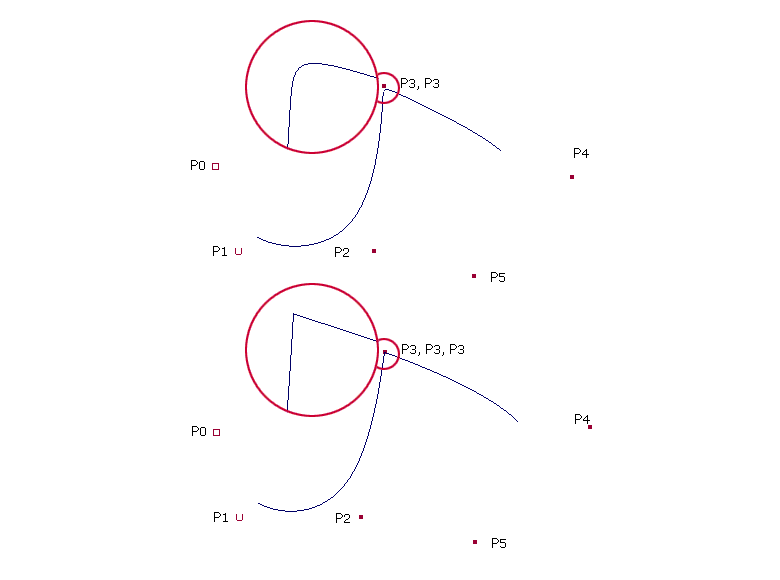 |
| Die Abbildung zeigt die Auswirkung auf die Kurve, wenn innerhalb zusätzliche Kontrollpunkte eingeführt werden: P3 als doppelten Kontrollpunkt: Durch einen zusätzlichen Kontrollpunkt schmiegt sich die Kurve näher an die Kontrollpunkte an. P3 als dreifachen Kontrollpunkt: Werden zwei Kontrollpunkte hinzugefügt, entsteht bei einer kubischen B-Spline eine Ecke. Allgemein gilt: Ein Eckpunkt entsteht, wenn die Anzahl der übereinanderliegenden Kontrollpunkte dem Grad der Kurve entspricht. |
Werden nichtuniforme Knotenwerte benutzt, sind die Basisfunktionen für jedes parametrische Intervall nicht mehr die selben. Die Anzahl von Knoten kann beliebig eingestellt werden und es können ungleiche Intervalle vorhanden sein. Der entscheidende Vorteil ist die erhöhte Flexibilität. Durch unterschiedlich große Intervalle entstehen verschiedene Gewichtsfunktionen in den jeweiligen Intervallen. Eine Mehrfachbestimmung eines Knotens führt zu feinen Veränderungen der Kurvenform.
 |
| Die Abbildung zeigt eine nichtuniforme B-Spline mit drei Kurvenabschnitten und die verwendeten Basisfunktionen. Am Anfangspunkt und am Endpunkt werden Mehrfachknotenwerte (Multiple End Knots) verwendet. Die Darstellung der Basisfunktion zeigt, dass die Basisfunktionen im Gegensatz zu den einer uniformen Kurve in den parametrischen Intervallen variieren. |
 |
| Die Abbildung zeigt zwei in Maya gezeichnete Nurbs-Kurven: (a) eine nichtuniforme B-Spline mit Knotenvektor [0,0,0,0,1,2,3,4,4,4,4] (a) eine nichtuniforme B-Spline mit Knotenvektor [0,0,0,0,1,2,3,3,3,4,4,4,4] |
Eigenschaften von B-Splines / Zusammenfassung
Die wichtigsten Eigenschaften der B-Splines:
- B-Splines besitzen n Kontrollpunkte. Eine Kurve wird mit n+1 Gewichtfunktionen beschrieben.
- Die Anzahl der Teilintervalle ist beliebig.
- B-Splines können Polynome mit beliebigen Graden verwenden.
- B-Splines besitzen Modellier-Eigenschaft mit lokaler Kontrolle: Jede Gewichtsfunktion ist über Teilintervalle definiert; daraus resultiert der lokale Einfluss.
- Teilintervalle werden durch Knotenvektoren bestimmt.
- Die Anzahl der Kontrollpunkte kann verändert werden ohne den Grad der Polynome zu verändern.
- Das Einfügen von Knoten und Kontrollpunkten ist eng miteinander verbunden.
- es werden uniforme und nichtuniforme B-Splines unterschieden:
| uniform | nichtuniform |
| Der Abstand zwischen jeweils zwei Knotenwerten ist immer konstant | Beliebige Werte für Knotenwerte und Intervalle sind möglich. |
| periodische Gewichtsfunktionen: alle Gewichtsfunktionen besitzen die gleiche Form und haben jeweils über ein gleich grosses Intervall Einfluss | Die Gewichtsfunktionen besitzen verschieden große Intervalle. Dadurch haben sie unterschiedlichen Einfluss auf die Kurve.td> |
| Mehrfachbestimmungen von Knotenwerten sind nicht möglich | Mehrfachbestimmung von Knotenwerten ist beliebig möglich, führt aber zur Reduzierung der Stetigkeit der Kurve. |
| Beispiel für Knotenvektor: [3,4,5,] | Beispiel für Knotenvektor: [0,1,2,3,3,4,5,] |
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen