Strahlenoptik für Beleuchtung, Reflexion und Transmission in der 3d-Grafik

Primäres Ziel in der 3d-Computergrafik ist in den meisten Fällen die Simulation reale Gegebenheiten. Dabei sind physikalische Gesetze Voraussetzung. In der 3d-Beleuchtung basieren die meisten Grundsätze und Annahmen auf den Gesetzen der Strahlenoptik. An dieser Stelle werden die für die 3d-Beleuchtung wichtigsten Gesetze in ihren Grundzügen beschrieben.

Das Reflexionsgesetz beschreibt, in welche Weise Lichtstrahlen durch eine spiegelnde Fläche reflektiert werden. Der einfallende Lichtstrahl wird dabei ohne sich aufzustreuen perfekt in die nach dem Reflexionsgesetz bestimmte Richtung gespiegelt.

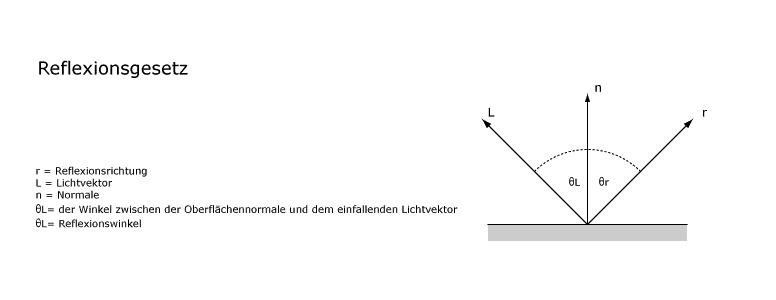Einfallswinkel und Reflexionswinkel haben den gleichen Betrag.

In der Realität existiert keine ideale spiegelnde Reflexion. Ein Lichtstrahl wird bei einer realen specularen Reflexion oder einer unvollkommenen spiegelnden Reflexion aufgespalten und in verschiedene Richtungen gestreut. Dabei entsteht ein vom Betrachtungswinkel v abhängiger Reflexionskegel. Ein weiteres physikalisches Reflexionsmodell ist die ideale oder vollkommene diffuse Reflexion. Dieses Reflexionsmodell beschreibt die perfekte gleichmäßige Streuung eines einfallenden Lichtstrahls in alle Richtungen mit gleicher Intensität. Die folgenden Abbildungen zeigen die in der 3d-Computergrafik verwendeten Reflexionsphänomene in einer 2d- Ansicht.

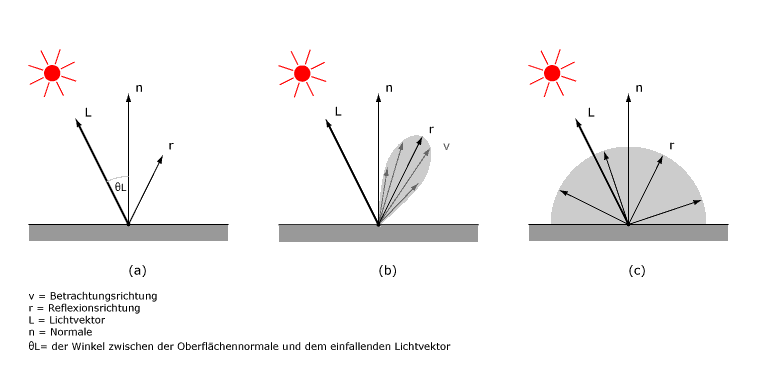Die drei in der Computergrafik verwendeten Reflexionsphänomene: (a) Ideale spekulare Reflexion (b) Reale spekulare Reflexion (c) Ideale diffuse Reflexion

Ideale spekulare Reflexion	Bei einer idealen Reflexion wird der einfallende Lichtstrahl ohne Abweichung perfekt in die nach dem Reflexionsgesetz bestimmte Richtung gespiegelt. Eine reale Oberfläche kann eine perfekte Reflexion realisieren.
Reale spekulare Reflexion	In der Realität wird ein Lichtstrahl bei einer realen spiegelnden Reflexion aufgespaltet und in verschiedene Richtungen gestreut. In Reflexionsrichtung entsteht ein Reflexionskegel.
Ideale diffuse Reflexion	Bei der diffusen Reflexion werden Lichtstrahlen in alle möglichen Richtungen gleich ausgesendet. Eine ideale diffuse Oberfläche reflektiert das Licht gleichmäßig in alle Richtungen. Eine solche Oberfläche wird in der Regel als matt bezeichnet. Theoretisch wird bei einer perfekten diffusen Oberfläche das Licht gleichmäßig in alle Richtungen zerstreut. In der Natur kommen jedoch keine perfekten Oberflächen vor, es gibt keine perfekt diffusen oder perfekt spiegelnden Oberflächen.

Bei der Lichtbrechung wird durch die Geschwindigkeitsänderung des Lichtes verursacht. Je optisch dichter das Medium ist, desto langsamer bewegt sich das Licht durch das Medium. Ein Lichtstrahl wird, wenn er von einem Medium in ein anderes übergeht, an der Grenzoberfläche zwischen beiden Medien gebrochen. Diese Brechung ist umso stärker, je flacher der Lichtstrahl auf die Grenzoberfläche zwischen den Medien auftrifft. Im optisch dichteren Medium nimmt der Lichtstrahl mit dem durch den Normalvektor gegebenen Lot einen kleineren Winkel ein. Im optisch dünneren Medium nimmt der Lichtstrahl einen größeren Winkel ein. Dieser Zusammenhang wurde 1621 erstmals von Snell beschrieben. Das Brechungsgesetz von Snell besagt, dass ein Lichtstrahl seine Richtung ändert oder gebrochen wird, wenn er von einem transparenten Medium in ein anderes übergeht. Das Gesetz gilt für alle Wellenarten.

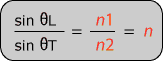n1 und n2 sind die Geschwindigkeiten des Lichtes in den entsprechenden Medien bzw. der Brechungsindex n ist der Brechungskoeffizient beim Übergang vom ersten in das zweite Medium. Die Brechungszahl (auch: Brechungsindex oder Index of Refraction) eines Mediums ist definiert als das Verhältnis der Geschwindigkeit von Licht im Vakuum zur Geschwindigkeit in diesem Medium. Folglich ergibt sich der Brechungskoeffizient zweier Medien aus dem reziproken Verhältnis ihrer Brechungszahlen. Die Brechungsindizes sind zusätzlich von der Wellenlänge und der Temperatur des Lichtes abhängig.

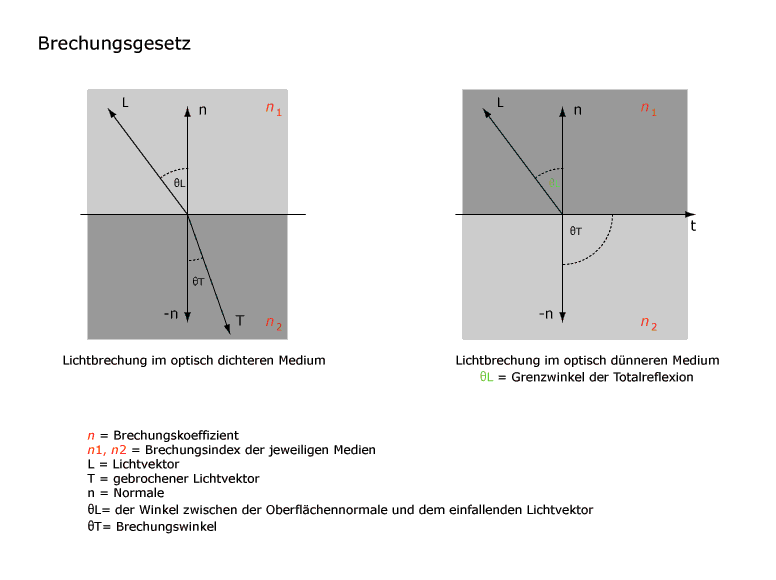Die linke Abbidlung zeigt eine Lichtbrechung vom optisch dünneren Medium in ein optisch dichteres Medium. Die rechte Abbildung zeigt den umgekehrten Fall. Ab einem bestimmten Winkel kommt es in diesem Fall zu einer Totalreflexion.

Die Totalreflexion wie in der oberen linken Abbildung ist ein spezielle Fall bei der Lichtbrechung. Tritt ein Lichtstrahl aus einem optisch dichteren Medium in ein optisch dünneres Medium über, wird dieser vom Lot gebrochen. Dies kann maximal bis 90° geschehen. In diesem Fall läuft der Lichtstrahl an der Grenze der beiden Medien entlang. Diesen Winkel nennt man Grenzwinkel der Totalreflexion, da bei einer weiteren Vergrößerung des Einfallswinkels keine Brechung mehr stattfindet. In diesem Fall wird das Licht nach dem Reflexionsgesetz reflektiert.

Die folgende Tabelle zeigt einige wichtige Brechungszahlen (Lichtbrechungsindex, IOR - Index of Refraction). Für den Einsatz in der Computergrafik sind die folgenden Zahlen ausschließlich Richtwerte.

Material	Lichtbrechungsindex
Luft (von Unterwasser)	0.75
Vakuum	1,0
Luft	1,0003
Eis	1,30
Wasser	1,33335
Alkohol	1.329
Glas	1,44
Quarz	1,55
Smaragd	1,57
Lapislazuli	1.61
Saphir	1,77
Rubin	1,77
Kristall	2,00
Diamant	2,43

Bei jeder Transmission bzw. Durchquerung eines Lichtstrahls durch ein transparentes Objekt kommt es zu einer zweifachen Anwendung des Brechungsgesetzes. Bei einer Glasscheibe mit geringer Stärke ist der Effekt vernachlässigbar. Der Betrachter sieht jedoch ein betrachtetes Objekt von seiner Originalposition verschoben.

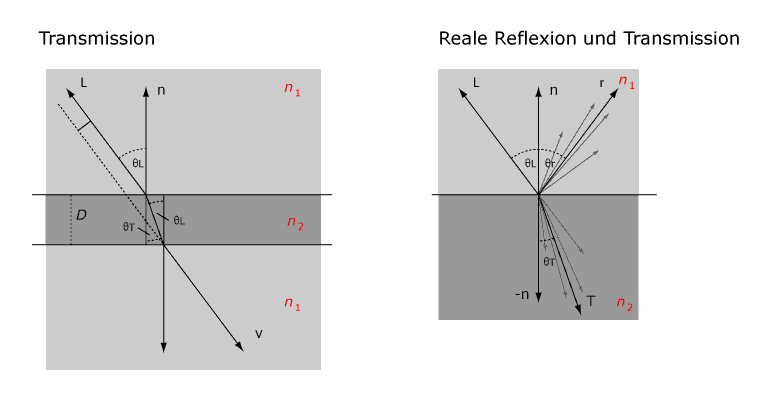Die linke Abbildung zeigt eine Transmission von einem optisch dünneren Medium durch ein optisch dichteres Medium. Hier ist neben dem Brechungsindex die Strecke D ausschlaggebend. Die rechte Abbildung zeigt eine reale Reflexion und Transmission. Einige Lichtanteile werden reflektiert, die meisten Lichtanteile werden in die ideale Reflexionsrichtung gespiegelt - reale spekulare Reflexion. Bei der Brechung wird nach dem selben Prinzip verfahren.