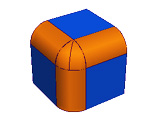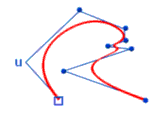
Das R in Nurbs steht für Rational. Nurbs-Kurven müssen aber nicht zwingend rational sein. In den meisten 3d-Programmen werden Nurbs-Kurven mit nicht-rationalen Eigenschaften verwendet.
Die entscheidenden Vorteile von rationalen Splines:
- rationale Splines bieten eine exakte Beschreibung für Kegelschnitte (wie Kreis und Ellipse).
Standardformen wie Kreis und Ellipsen können mittels Polynome nie exakt definiert werden. Bézier-Kurven und B-Splines können Grundkörper wie Kreise und Ellipsen nur durch Annäherung definieren. Rationale Kurven können diese exakt mathematisch definierten Grundformen beschreiben. Vereinfacht dargestellt entstehen rationale B-Splines in der 3d-Computergrafik durch die Projektion einer nicht-rationalen B-Spline-Kurve im affinen 3d-Raum. Das Ergebnis ist die sogenannte Nurbs-Kurve.
- Nurbs-Kurven erlangen duch die rationale Eigenschaft Kontrollpunktgewichte
Rationale B-Splines sind durch vierdimensionale Kontrollpunkte definiert. Jeder Kontrollpunkt erhält dadurch eine zusätzliche Eigenschaft bzw. einen zusätzlichen Formparameter, der als Gewicht bezeichnet wird. Die Gewichtung eines Kontrollpunktes beeinflußt nur den Kurvenabschnitt, den auch der Kontrollpunkt beeiflusst. Die Kurve wird umso näher an den Kontrollpunkt hingezogen, je höher das Gewicht des Kontrollpunktes wird.
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel