In der 3d-Computergrafik hat sich neben der Bézier-Kurve die Nurbs-Kurve als Standard etabliert. Viele 3d-Programme wie Maya, Cinema oder 3dsmax bieten sowohl Bézier-, als auch Nurbs-Kurven. Programme wie Studio Tools oder Rhinoceros arbeiten ausschließlich mit Nurbs-Kurven. Dieses Kapitel befasst sich mit den Vorteilen von rationalen Kurven und allgemeingültige Aspekte zu Nurbs-Kurven.
Das R in Nurbs steht für Rational. Nurbs-Kurven müssen aber nicht zwingend rational sein. In den meisten 3d-Programmen werden Nurbs-Kurven mit nicht-rationalen Eigenschaften verwendet.
Die entscheidenden Vorteile von rationalen Splines:
- rationale Splines bieten eine exakte Beschreibung für Kegelschnitte (wie Kreis und Ellipse).
Standardformen wie Kreis und Ellipsen können mittels Polynome nie exakt definiert werden. Bézier-Kurven und B-Splines können Grundkörper wie Kreise und Ellipsen nur durch Annäherung definieren. Rationale Kurven können diese exakt mathematisch definierten Grundformen beschreiben. Vereinfacht dargestellt entstehen rationale B-Splines in der 3d-Computergrafik durch die Projektion einer nicht-rationalen B-Spline-Kurve im affinen 3d-Raum. Das Ergebnis ist die sogenannte Nurbs-Kurve.
- Nurbs-Kurven erlangen duch die rationale Eigenschaft Kontrollpunktgewichte
Rationale B-Splines sind durch vierdimensionale Kontrollpunkte definiert. Jeder Kontrollpunkt erhält dadurch eine zusätzliche Eigenschaft bzw. einen zusätzlichen Formparameter, der als Gewicht bezeichnet wird. Die Gewichtung eines Kontrollpunktes beeinflußt nur den Kurvenabschnitt, den auch der Kontrollpunkt beeiflusst. Die Kurve wird umso näher an den Kontrollpunkt hingezogen, je höher das Gewicht des Kontrollpunktes wird.
Nurbs bedeutet Non-Uniform-Rational B-Splines (nichtuniforme rationale B-Splines).
Im Gegensatz zu Polygonnetzen mit vielen Dreiecksflächen werden die Nurbs- Flächen und -Kurven mathematisch beschrieben. Die Kanten erscheinen nicht facettiert. Nurbs-Kurven und -Flächen gelten besonders in Flächenmodellierungsprogrammen wie Rhinoceros, Maya oder Studio Tools als die Standardbeschreibung für Kurven und Flächen. Nurbs-Kurven und die daraus generierten Nurbs-Flächen verhalten sich ähnlich und haben eine gemeinsame Terminologie. Eine Nurbs-Kurve wird durch vier Eigenschaften definiert:
- Grad
- Kontrollpunkte
- Knoten
- Gewichtung.
Der Vorteil liegt vor allem bei der Berechnung sehr glatter Oberflächen und in der interaktiven Handhabung der B-Splines. Die entscheidenden Vorteile:
- Interaktives Platzieren und Bewegen von Kontrollpunkten
- Interaktives Platzieren von Knotenpunkten
- Interaktives Steuern der Kontrollpunkt-Gewichte
- lokale Kontrolle
- exakte Bearbeitungsfunktionen (Trimmen, Boolschen, Fillet, ...)
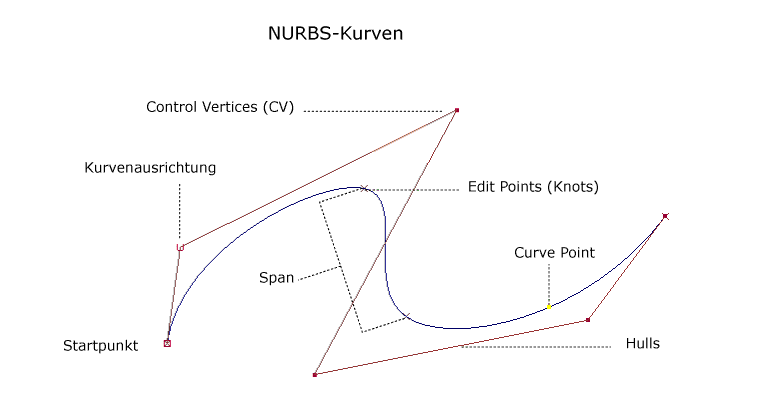 |
| Die Anatomie einer Nurbs-Kurve am Beispiel Maya: Control Vertex, Kontrollpunkte (CV) |
- Der Grad einer Nurbs-Kurve wird als positive Ganzzahl angegeben.
- Ordnung der Kurve = Kurvengrad + 1 (Grad 1 = linear, Grad 2 = quadratisch, Grad 3 = kubisch ,Grad 5 = quintisch)
- Der Grad einer Kurve ist der höchste Exponent, der für die Darstellung der Kurve verwendeten Polynome.
- NURBS-Kurven werden in den meisten 3d-Computerprogrammen durch lineare Polynome (eckige Kurven) bzw. duchr kubische Polynome (rund) repräsentiert. Nurbsflächen mit Polynome höheren Grades werden in Computeranimationsprogrammen eher selten eingesetzt. In CAD-Programmen wie StudioTools oder Catia werden Nurbs-Kurven bis 7 Grades eingesetzt.
- Bei Kurve höheren Grades haben die Kontrollpunkte weniger Einfluss auf die Kurve haben. Die Kontrollpunkte müssen mehr bewegt werden, um die Kurve in gleichem Ausmaß zu verändern als eine Kurve niedrigeren Grades. Eine Kurve niedrigeren Grades schmiegt sich näher an die Kontrollpunkte an.
- Kurven niedrigeren Grades sind weniger rechenintensiv.
- Im Gegensatz zu Bézier-Kurven ist der Grad bei Nurbs-Kurve unabhängig von den Eingabepunkten. (siehe B-Spline bzw. Bézier-Kurven)
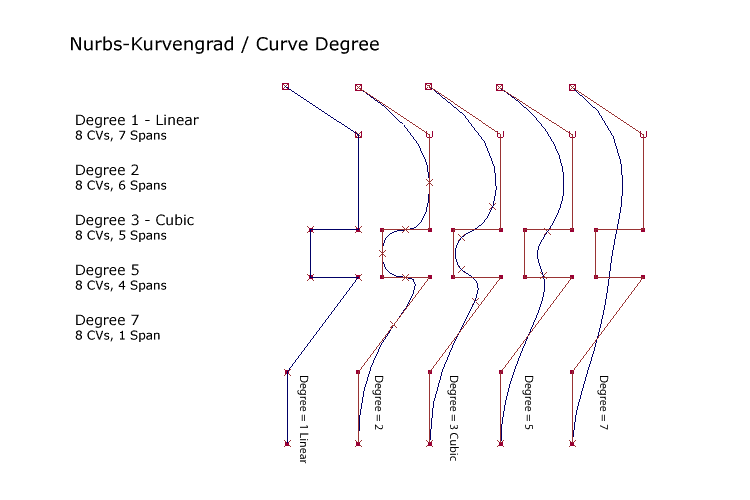 |
| Nurbs-Kurven mit unterschiedlichen Graden in dem Programm Maya. |
Nurbs-Kurven können mit Kontrollpunkten gezeichnet und bearbeitet werden. Jeder Kontrollpunkt hat eine angegliederte Zahl, die Gewicht genannt wird. Wenn die Kontrollpunkte einer Kurve alle dieselben Gewichte (normalerweise 1) haben, wird die Kurve nicht-rational genannt. Sind die Knotenpunkte mit unterschiedlichen Gewichten ausgestattet, wird eine Kurve rational genannt. Bei Nurbs-Kurve besteht die Möglichkeit, Kontrollpunkt-Gewichte zu variieren. Eine Nurbs-Kurve kann, muss aber nicht unbedingt rationale Eigenschaften haben. In der Praxis sind die meisten NURBS-Kurven, die in den 3d-Programmen verwendet werden, nicht-rational.
Knoten sind eine Liste von Zahlen: Grad der Kurve +N-1, wobei N die Anzahl Kontrollpunkte ist. Eine Zahlenliste von Knotenwerten wie [0,0,0,1,2,3,3,3] wird auch Knotenvektor genannt. Bei diesem Vektor handelt es sich nicht um keinen XYZ-Vektor, sondern um eine Liste von Knotenwerten - Ganzzahlen.
Mehr Informationen zu Knotenwerten und Knotenvektor: B-Spline
Nurbskurven können sowohl durch Kontrollpunkte bzw. Knotenpunkte erzeugt als auch bearbeitet werden..
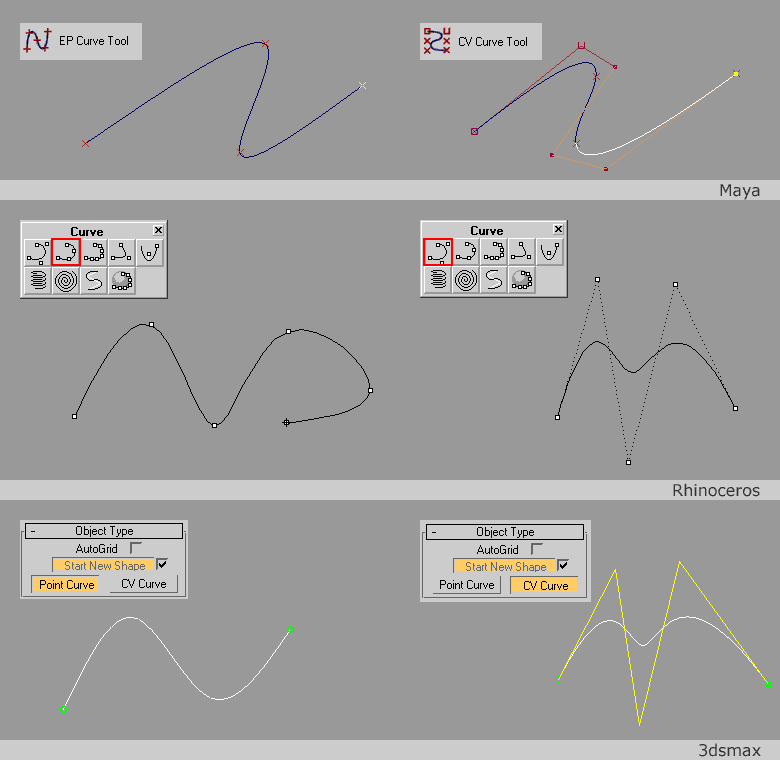 |
| 3d-Programme bieten unterschiedliche Zeichenwerkzeuge für Nurbskurven. Werden Kurven mit Knotenpunkten generiert wird in Maya das EditPointTool und in 3dsmax die Ponit Curve verwendet. In Rhinoceros werden bei einer Control Point Curve bzw. in 3dsmax mit der CV Curve Kontrollpunkte positioniert. |
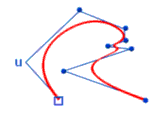
NURBS-Kurven und Flächen besitzen zusätzlich zu den Koordinaten im 3d-Raum, in dem sie angezeigt werden, einen Parameterraum. Eine Gruppe von Werten, die als Knoten bzw. Knots bezeichnet werden, definieren den Einflussbereich jedes Kontrollpunktes (CV) auf der Kurve oder Fläche. Der Parameterraum für Kurven ist eindimensional und wird als U-Parameter bezeichnet. Dieser Wert erstreckt sich vom Anfangspunkt bis zum Endpunkt einer Nurbs-Kurve. Flächen besitzen zwei Dimensionen im Parameterraum, die als u-Parameter und v-Parameter definiert werden. Der Parameterraum einer Nurbs-Kurve hat erheblichen Einfluss auf dei Nurbsfläche.
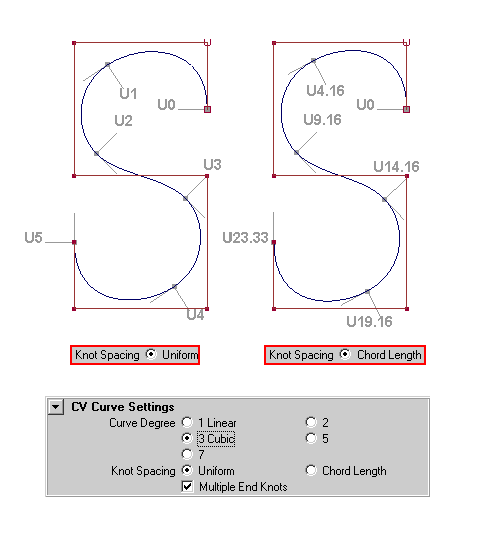 |
| Die Abbildung zeigt ein Beispiel für den Parameterraum für Nurbs-Kurven in dem Programm Maya. Das Programm bietet beim Erstellen einer Nurbs-Kurve zwei Möglichkeiten: |
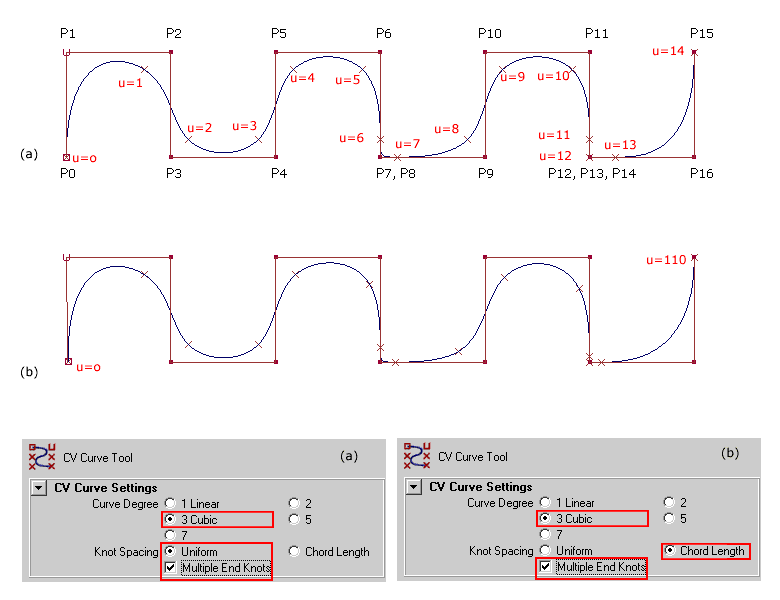 |
| (a) |
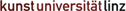
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen