
Fourier hat herausgefunden, dass sich sämtliche periodische Funktionen f(x) durch eine Summe von Sinus und Cosinus Funktionen annähern lassen (in Wirklichkeit müssen mehrere Kriterien erfüllt werden, doch das ist für dieses Beispiel irrelevant). Die Formel für diese Annäherung sieht folgendermaßen aus:
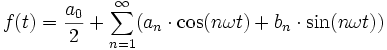
Dabei sind ![]() und a0 ein konstanter Anfangswert.
und a0 ein konstanter Anfangswert.
Die Koeffizienten an und bn können folgendermaßen berechnet werden:
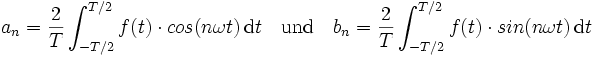
Beispiel Rechtecksfunktion
Im Folgenden wird die Fourier-Reihe anhand einer Rechtecksfunktion betrachtet (siehe Grafik).
Gegeben: Rechtecksfunktion f(x)
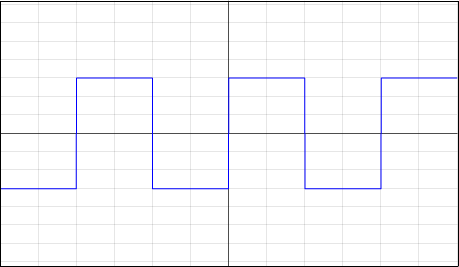
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx )
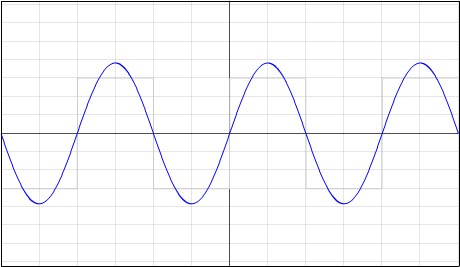
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) )
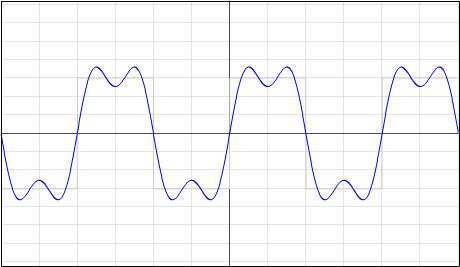
Sieht man sich die Formel an, bemerkt man, dass die Funktion f(x) hier sehr stark vereinfacht werden konnte (verglichen mit der allgemeinen Formel). Die Koeffizienten für die Cosinus-Schwingungen betragen 0, deswegen werden sie auch nicht mehr aufgelistet. Die 0 ergibt sich, wenn man in die Formel an einsetzt. Für die Koeffizienten der Sinus-Schwingungen wurde in die Formel bn eingesetzt. Die Abweichungen von der allgemeinen Formel resultieren aus den bereits angesprochenen Vereinfachungen.
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) + 1/5 * sin(5x) )
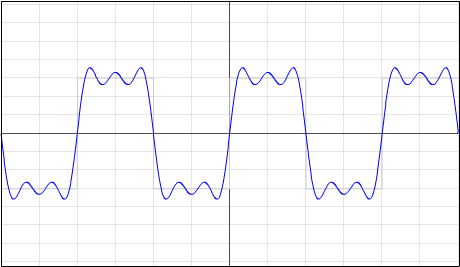
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) + 1/5 * sin(5x) + 1/7 * sin(7x) )
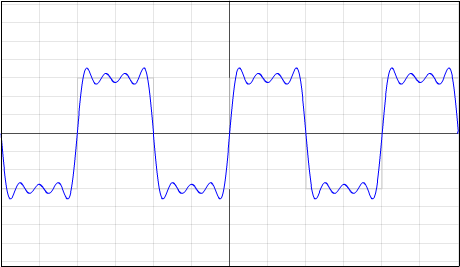
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) + 1/5 * sin(5x) + ... + 1/12 * sin(12x) )
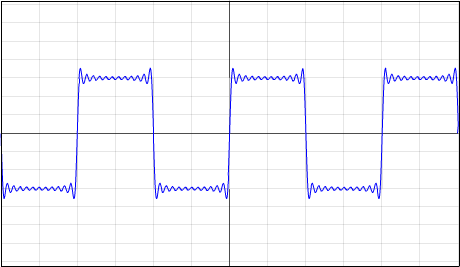
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) + 1/5 * sin(5x) + ... + 1/25 * sin(25x) )
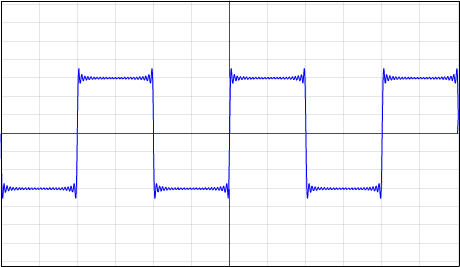
Gegeben: Rechtecksfunktion f(x)
Ergebnis: f(x) = 4*3/PI * ( sinx + 1/3 * sin(3x) + 1/5 * sin(5x) + ... + 1/100 * sin(100x) )
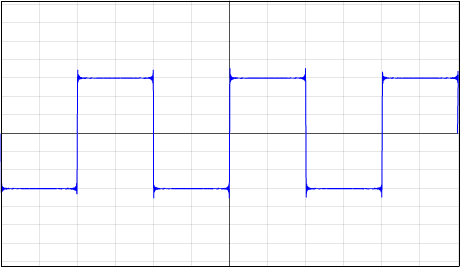
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen voriges Kapitel
voriges Kapitel