
|
Wavelets sind Funktionen die ganz bestimmte mathematische Kriterien erfüllen, man kann Wavelet demnach nicht als Kompressionsalgorithmus ansehen. Die Wavelet-Kompression, die in diesem Modul vorgestellt wird, bedient sich der Vorteile von Wavelets, doch dazu später noch mehr.
Um die Funktionsweise des Algorithmus verstehen zu können, muss man zuerst die Grundzüge der Wavelets verstanden haben.
Nach einer kurzen Entwicklungsgeschichte werden Wavelets (kurz) erklärt, danach das Kompressionverfahren in beide Richtungen vorgestellt und schließlich mit einem Beispiel anschaulich gemacht.
Die Wavelet-Analyse besteht im Prinzip darin, eine Prototypfunktion (auch analysierendes Wavelet oder Mutterwavelet genannt) zu adaptieren. Die zeitliche Analyse wird dabei mit einer hochfrequenten Variation der Prototypfunktion durchgeführt, wohingegen bei der Frequenzanalyse eine niederfrequente Variante desselben Wavelets verwendet wird.
Nachdem das ursprüngliche Signal bzw. Funktion mit einem Binärbaum von Koeffizienten dargestellt werden kann, reichen diese Koeffizienten aus um die ursprünglichen Daten wieder herzustellen. Wenn man nun eine geeignete Wavelet-Funktion wählt (angepasst an die Daten), oder die Koeffizienten unterhalb eines gewissen Wertes abschneidet (was im Prinzip einem Verzicht auf Details gleichkommt), können die Daten tatsächlich komprimiert werden.
Nichtsdestotrotz, bei der Wavelet-Analyse spielt der Skalierungsfaktor, mit dem man die Daten betrachtet, eine große Rolle. Wavelet-Algorithmen verarbeiten die Daten in einer bestimmten Skalierung bzw. Auflösung. Das Resultat ist -metaphorisch gesprochen- dass man bei der Wavelet-Analyse sowohl die Bäume als auch den Wald betrachtet.
Genau dieser Umstand macht Wavelets interessant und nützlich. Wissenschaftler suchen schon seit Jahrzehnten nach geeigneteren Funktionen als Sinus und Cosinus (die Grundlage für die Fourier-Reihe), um unregelmäßige Signale anzunähern. Die Definition von Sinus und Cosinus besagt, dass sie nicht lokale Funktionen sind, die sich bis zur Unendlichkeit erstrecken. Sie sind also nicht besonders gut geeignet, um einmalige, scharfe Spitzen darzustellen. Mit Wavelet-Analyse allerdings wird es möglich, Funktionen zu verwenden, die sehr schön in endliche Bereiche eingebettet sind. Sie sind demnach sehr gut dazu geeignet, stark unregelmäßige Funktionen zu beschreiben.
Die genauere Entwicklungsgeschichte ist für dieses Einführungsmodul nicht relevant.
Grundsätzlich gibt es nur eine Wavelet-Transformation. Was sich allerdings unterscheidet, sind die Wavelets, die man für die Transformation wählen kann. Hierbei gilt: je besser das Wavelet zu den zu komprimierenden Daten passt, desto besser das Ergebnis.
Hier ein paar mögliche Wavelets:
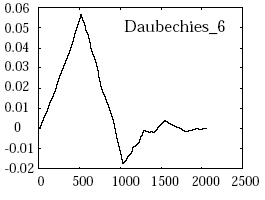
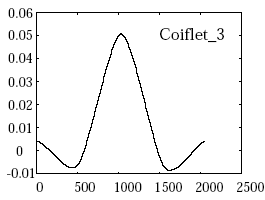
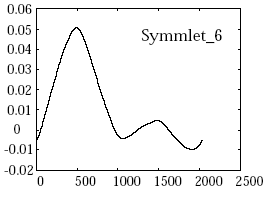
Welches Wavelet auch immer gewählt wird, der Ausgangspunkt ist eine Gruppe von N Werten. Dabei ist zu beachten, dass die hier vorgestellte Kodierung sehr vereinfacht ist. Ziel dabei ist nicht, die Mathematik hinter Wavelets im Detail zu erfassen, sondern das Prinzip dahinter zu verstehen.
Es wird ein Binärbaum mit ![]() Werten erstellt. Dabei werden jeweils 2 Werte genommen und deren arithmetisches Mittel berechnet. Aus den Werten
Werten erstellt. Dabei werden jeweils 2 Werte genommen und deren arithmetisches Mittel berechnet. Aus den Werten ![]() und
und![]() ergibt sich also folgender neuer Knoten:
ergibt sich also folgender neuer Knoten: ![]() .
.
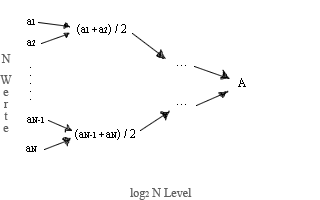
Nun wird dem Baum noch eine Information hinzugefügt, und zwar jeweils an den Kanten (in obiger Abbildung durch die Pfeile dargestellt): die Differenz zwischen dem Punkt an der Pfeilspitze und dem Punkt am Pfeilschaft – auch Distanzen zwischen den Knoten genannt.
Wie man aus der obigen Abbildung auch entnehmen kann, sind die Distanzen die von einem Knoten ausgehen, jeweils entgegengesetzte Werte, weil der Durchschnittswert von den zwei Werten den gleichen Abstand hat. (zum Beispiel: Der Durchschnitt von 2 und 8 ist 5, welches eine Distanz von -3 zu 2 und +3 zu 8 bedeutet.)
Im Augenblick wurde noch keine Zerlegung erreicht. Im Gegenteil sogar, die Struktur ist gewachsen von einem Vektor aus N Werten zu einem Baum mit ![]() Werten für die Knoten plus
Werten für die Knoten plus ![]() Werte für die Kanten! Der nächste Schritt besteht daher aus der Wahl eines Baumlevels – d.h. eines Zerlegungslevels p zwischen 1 und
Werte für die Kanten! Der nächste Schritt besteht daher aus der Wahl eines Baumlevels – d.h. eines Zerlegungslevels p zwischen 1 und ![]() (dem Maximum an möglichen Levels). Ein Level wird hierbei gebildet aus Knotenwerten und den unteren Kanten, die daraus hervorwachsen.
(dem Maximum an möglichen Levels). Ein Level wird hierbei gebildet aus Knotenwerten und den unteren Kanten, die daraus hervorwachsen.
Wurde der Zerlegungslevel gewählt, erhält man die level-p-komprimierten Werte (mit ![]() ), indem man nacheinander die Level 1 bis inklusive p durchrechnet. Dieses Prinzip sollte im Beispiel klarer werden.
), indem man nacheinander die Level 1 bis inklusive p durchrechnet. Dieses Prinzip sollte im Beispiel klarer werden.
Einmal zerlegt, ist es ein leichtes, die Ausgangswerte wieder herzustellen. Man muss lediglich die Operation umkehren. Es ist wichtig anzumerken, dass die Skalierungsfaktoren dieses Levels genauso aufrecht erhalten werden müssen wie die Detail-Koeffizienten, um die Ausgangswerte in einem Level p wiederherstellen zu können.
Redet man hierbei von Skalierungsfaktor, so ist der Durchschnitt gemeint, das Wort Detail-Koeffizient beschreibt die Distanz.
Für dieses Beispiel wird der Einfachheit halber ein linear codiertes Bild in einer Auflösung von 4x4 Pixeln in 16 Graustufen zwischen 0 und 15 verwendet.
| Ausgangsbild: | 7 | 11 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 10 | 9 | 5 | 12 | 12 | 12 | 12 |
| Level 1 | 9 | 5 | 5 | 5 | 9 | 7 | 12 | 12 | ||||||||
| 2 | 0 | 0 | 0 | 1 | -2 | 0 | 0 | |||||||||
| Level 2 | 7 | 5 | 8 | 12 | ||||||||||||
| -2 | 0 | -1 | 0 | |||||||||||||
| Level 3 | 6 | 10 | ||||||||||||||
| -1 | 2 | |||||||||||||||
| Level 4 | 8 | |||||||||||||||
| 2 | ||||||||||||||||
In der obigen Tabelle beschreibt die obere Zeile jeweils den Skalierungsfaktor, die untere den Detailkoeffizienten.
Wird Zerlegungslevel 3 gewählt, so speichert man die Skalierungsfaktoren (6, 10) und alle Detail-Koeffizienten der Level 3, 2 und 1. (Die Koeffizienten von Level 0 brauchen nicht gespeichert zu werden, da sie immer alle implizit 0 sind!)
 Verlauf
Verlauf

 Alle Kapitel anzeigen
Alle Kapitel anzeigen